Who is incorrect? - Part 1

This problem involved four individuals from real/virtual worlds: Alice, Bob, Catherine and Dorothy.

Before starting the problem, let me introduce each of them first, for later problems:

Alice is a naive and innocent 7-year-old girl in Alice in wonderland . She comes from England. She haven't taken any of the math classes, and she can't even recite the multiplication table. Naive as she is, she has a clear intuition for math. Even though she can't exactly figure it out due to bad calculation skills, she can tell whether it is correct or incorrect.

Bob is an 18-year-old senior high school student in a(n) (in)famous senior high school in China. He always gets over 140 points on math in every mock exam, and he is one of the top students in the whole class. He is very skilled in calculation and he can solve an Analytic Geometry problem in a matter of minutes. However, he only studies what are told and what may appear in Gaokao, knowing nothing other than that. What's worse, he doesn't like to derive and prove formulas since he only recites them for exams and has no idea why. As a result, he has nearly no intuition for math and he doesn't even know how to test a solution to a system of equations.

Catherine is a premium member in brilliant.org and she has purchased the lifelong pack for it. She comes from France, 60-year-old. She has finished all courses in it, including Logic, Number Theory, Discrete Mathematics, Linear Algebra, Multivariable Calculus and Differential Equations. In other words, she has finished the relatively fundamental parts of modern math. Although she may solve simple problems in a hard way, she has an indeed deep understanding of math.

Dorothy is a clever 13-year-old American girl in The Wizard of Oz . She is very skilled in competitive math contests such as AMC, and has got several gold medals. At one time, she even got all the problems correct elegantly. She is especially good at using different techniques in solving complex equations, inequalities, integration and discrete mathematics. Not only does she know how to use these, but also knows exactly why it works. Of course, she also has very good intuition for math.

You may already choose who is incorrect just by the description. But let's give each of them a shot, why not?

Somehow, they form a group to take part in a contest. The contest is to see who can solve the latest problem on brilliant.org as fast as possible. Each of them will take turns to translate and solve the problem.

One day, it was Bob's turn and the problem read:

Given that $\begin{cases} 1 \leq x+y \leq 3 && ① \\ -1 \leq x-y \leq 1 && ②\end{cases}$

What is the range of $4x+2y$ ?

The range can be expressed as $[l,r]$ . Submit $l+r$ .

Bob immediately got down to the problem and after a minute, he got his answer and said to his partners:

The answer is $12$ . My solution is as follows:

$①+②$ gives $0 \leq 2x \leq 4$ , then $0 \leq 4x \leq 8. \qquad ③$

$② \times (-1)$ gives $-1 \leq y-x \leq 1. \qquad ④$

$①+④$ gives $0 \leq 2y \leq 4. \qquad ⑤$

Substitute $③+⑤$ into $4x+2y$ gives $0 \leq 4x+2y \leq 12$ , $l=0, r=12$ , hence the result $12$ .

As Bob taking lead to submitting the answer (Well, in this contest, you only have one try), Alice stopped him at once and said:

No, this solution is incorrect.

First, since it's a problem on this contest, it won't be that easy and let you think like that.

Second, you are essentially breaking $x$ and $y$ apart and ignoring their relations.

Third, no matter how hard I try a pair of $x,y$ so that $4x+2y=0$ or $12$ , it doesn't work. Maybe I'm not so good at calculation, but I believe that your solution is incorrect.

But Alice didn't find the solution after a short time. Bob didn't listen to her and submitted the answer. Surprisingly, it says "Correct!". Feeling confused, she then counseled Dorothy.

Dorothy was also trying this problem and saw Bob writing his solution, and then she said:

Bob, your initial thought is correct, but you are doing it in a wrong way and your range is incorrect. Coincidentally, due to some flaws of this problem, your submitted answer happens to be the same.

The key point is to break $4x+2y$ into linear combinations of $x+y$ and $x-y$ , in order to maintain the relationship between $x+y$ and $x-y$ .

Let $4x+2y=a(x+y)+b(x-y)$ , compare the coefficients and solve for $a,b$ gives us:

$4x+2y=3(x+y)+(x-y)$ .

From given conditions we have:

$\begin{cases} 3 \leq 3(x+y) \leq 9 && ③ \\ -1 \leq x-y \leq 1 && ④\end{cases}$

Adding together gives us $2 \leq 4x+2y=3(x+y)+(x-y) \leq 10$ , $l=2, r=10$ , and the answer is $12$ .

I think we're very lucky. If the author change the way of submitting the range, it would be different.

Bob felt relieved as he didn't mess this up so he didn't think about it any longer. After all, they both got the "same" answer, there would be some possibility that Dorothy was wrong. So Bob insisted that he was right. Just then, Catherine began using Geogebra and said:

This problem is a linear programming problem . It can be done using the Convex Optimization Algorithm.

Here's the graph:

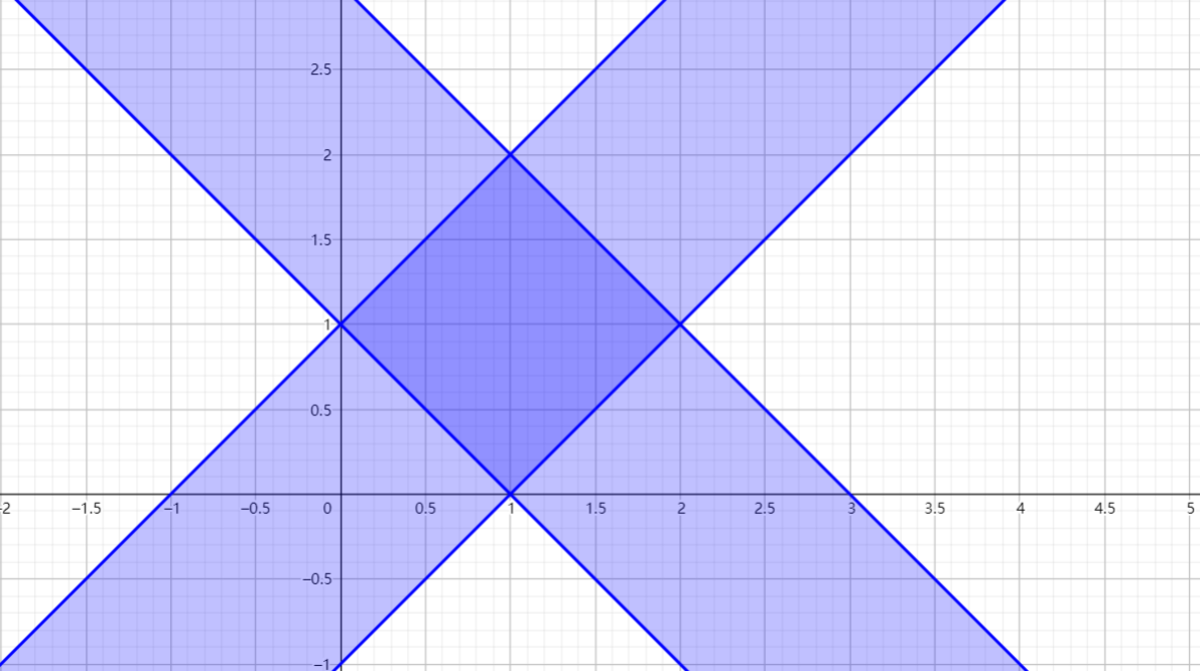
Now according to what they said, who is incorrect ?