Who is incorrect? - Part 2

This is sequel to Who is incorrect? - Part 1 .

One day, Alice, Bob, Catherine, Dorothy encountered a problem they hadn't seen before except Bob:

Angle $\alpha, \beta \in (0,\pi)$ , $\tan(\alpha-\beta)=\dfrac{1}{2}, \tan \beta=-\dfrac{1}{7}$ .

Find the sum of all possible values for $2\alpha-\beta$ in radians.

If the sum can be expressed as $S$ , Submit $\lfloor 1000S \rfloor$ .

Bob was very excited and within a minute he figured out the result. He said:

The answer is $\boxed{2356}$ . I've seen this a lot in Chinese math tests, so it's a piece of cake. Here's my approach:

The key is to break $2\alpha-\beta$ into $\alpha + (\alpha-\beta)$ , $\alpha$ into $(\alpha-\beta)+\beta$ , instead of using addition formula twice or solving the equation in order to reduce calculations.

$\tan \alpha =\tan((\alpha-\beta)+\beta)=\dfrac{\tan(\alpha-\beta)+\tan \beta }{1-\tan(\alpha-\beta)\tan \beta}=\dfrac{1}{3}$ .

Then we just need to find $\tan(2\alpha-\beta)$ .

$\tan(2\alpha-\beta)=\tan(\alpha + (\alpha-\beta))=\dfrac{\tan \alpha +\tan(\alpha-\beta)}{1-\tan \alpha \tan(\alpha-\beta)}=1$ .

Since $\alpha, \beta \in (0,\pi)$ , $2\alpha-\beta \in (-\pi,2\pi)$ , $\tan(2\alpha-\beta)=1$ , from the property of tangent function we get $2\alpha-\beta$ could be $-\dfrac{3\pi}{4}, \dfrac{\pi}{4}, \dfrac{5\pi}{4}$ , sum these up and we will get $S=\dfrac{3\pi}{4}$ , $\lfloor 1000S \rfloor=\boxed{2356}$ .

As Bob was proud of his technique, Alice kept him from typing the answer and said:

Well, I know little about the formulas of trigonometry. But judging from processing above and the value of $\tan \alpha$ , $\tan \beta$ , considering the ranges of $\alpha, \beta$ , it is guaranteed that $\alpha ,\beta, 2\alpha-\beta$ has one and only one value. Although I can't figure them out, $2\alpha-\beta$ indeed has only one solution.

Alice has little knowledge that $\tan \alpha, \tan \beta$ is related to slopes (Actually, it's quite impressive for such a little girl). Right now Alice drew the following graph using Geogebra :

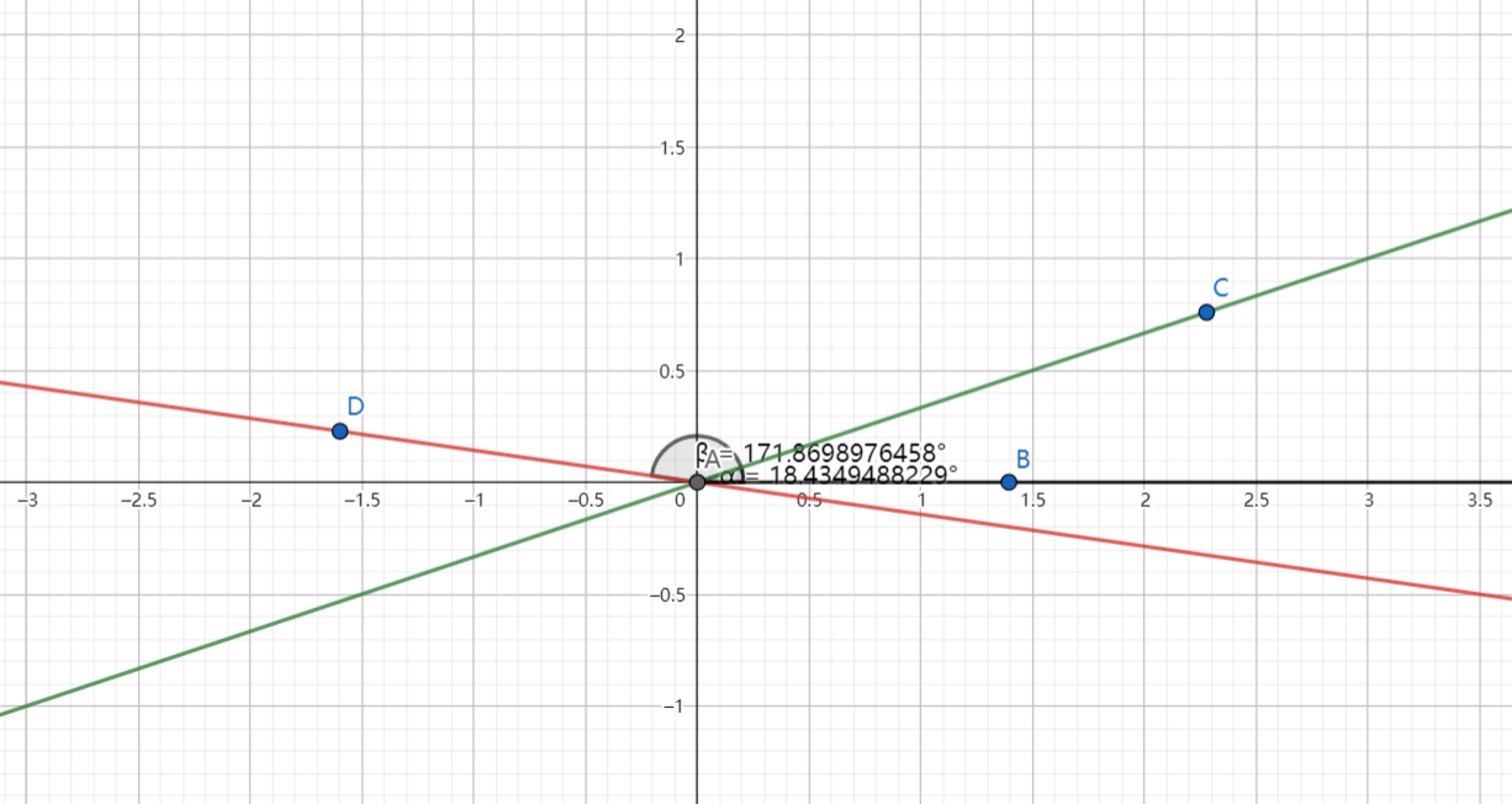
Bob took some calculation and slightly believed that it indeed has only one solution, so he listened to her this time.

But Alice wasn't satisfied with the graph method. She wanted to see a more religious proof without using graphs.

She asked Dorothy and Dorothy said:

Bob, I'm actually quite impressed at your calculation skills and technique learnt from Chinese exams. Your work saved me a lot of time. But to be honest, you lack clear intuition for math. Math isn't just about calculations. Math means a LOT MORE than that. If you really want to travel further on math, you're going to have to do much better than that. For this problem, I think you will find this pertinent:

Just according to Alice's graph, it's definite that it has only one solution. The problem said "find all possible values", it's quite easy for those paralyzed by exams to fall into a multi-solution trap. But the wording is actually right, since one solution is also regarded as a possible solution.

To state this more formally, we can do like this:

Since $\tan \alpha = \dfrac{1}{3} < \dfrac{\sqrt{3}}{3} = \tan \dfrac{\pi}{6}$ ,

$0< \alpha <\dfrac{\pi}{6}$ , $0 < 2\alpha < \dfrac{\pi}{3}$ .

$\tan \dfrac{5\pi}{6}=-\dfrac{\sqrt{3}}{3} < \tan \beta = -\dfrac{1}{7} < 0 = \tan \pi$ ,

thus $\dfrac{5\pi}{6}<\beta<\pi$ .

Adding together gives us $-\pi<2\alpha-\beta<\dfrac{\pi}{2}$ , since $\tan(2\alpha-\beta)=1$ and it's range bound to a interval so that $\tan(2\alpha-\beta)=1$ has only one solution, it means that $2\alpha-\beta=-\dfrac{3\pi}{4}$ , thus $\lfloor 1000S \rfloor=\boxed{-2357}$ .

Everyone agreed with the solution by Dorothy (of course, with the little help of Bob). But Catherine has her own ideas:

According to the graph, It's evident that $2\alpha-\beta$ must less than zero, so the range narrows to $(-\pi,0)$ .

Why not consider calculating $\sin(2\alpha-\beta), \cos(2\alpha-\beta)$ to specify the exact angle since within this range?

Since if $\sin(2\alpha-\beta), \cos(2\alpha-\beta)$ are found, the angle would be unique.

According to what they said, who is incorrect ?

Remember, we are finding whose answer is incorrect, not considering the complexity and steps they will need.