Whole Circle in a Quarter Circle
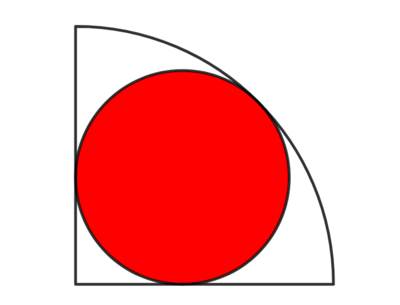
A circle is inscribed in a quarter circle. The ratio of the (red) circle's area over the area of the quarter circle can be written as ( b + c ) 2 a with all of the variables being integers.
Find a + b + c .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
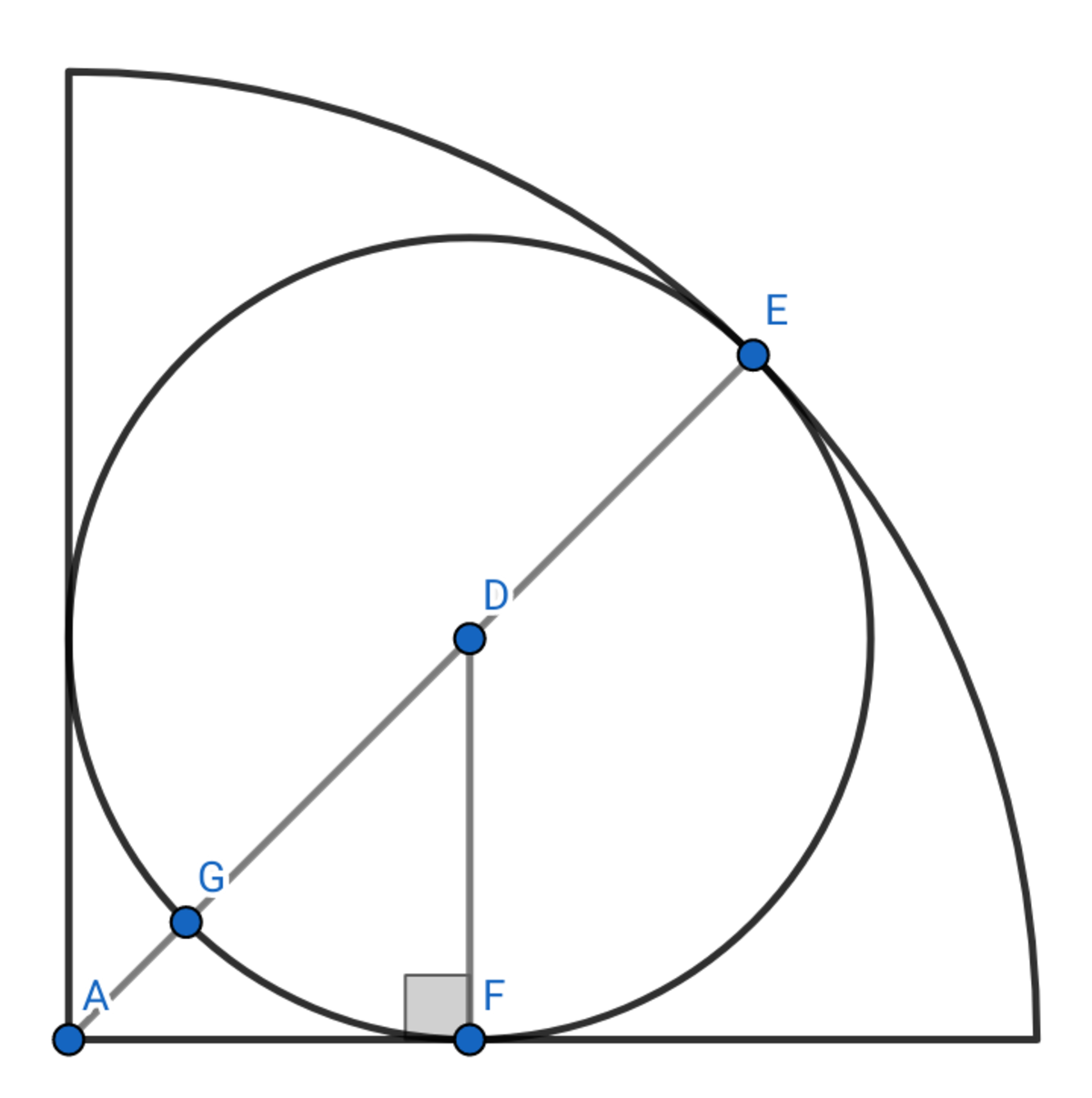
Let the radius of the quarter circle be a and the radius of the inscribed circle be b . Line segment A E is equal to a . Line segments E D , F D , G D , and A F are all equal to b .
We see that A D is equal to a − b . Since it is the hypotenuse of an isosceles right triangle, we can set up an equality.
A D 2 ( a − b ) 2 a 2 − 2 a b + b 2 ⟹ a = A F 2 + D F 2 = b 2 + b 2 = 2 b 2 = b + b 2
The area of the quarter circle is equal to 4 π a 2 or 4 π ( b + b 2 ) 2 while the area of the inscribed circle is π b 2 . The needed ratio would then be:
4 π ( b + b 2 ) 2 π b 2 = π ( b + b 2 ) 2 4 π b 2 ⟹ ( 1 + 2 ) 2 4
Thus, ( b + c ) 2 a ⟹ a = 4 , b = 2 , c = 1 . The sum of the variables would then be 7 .
Good solution. Note that the inscribed circle is tangent to the quarter circle at 3 points and D is the point ( r , r ) , where r is the radius of the inscribed circle. Say, without loss of generality, that the radius of the quarter is 1 , so r + r 2 + r 2 = 1 and r = 1 + 2 1 which gives the same result.

Let the radius of the circular quadrant be 1 and that of the red circle be r . Then we note that
2 r + r ⟹ r = 1 = 2 + 1 1
Then the ratio of the area of the red circle to the area of the quadrant
4 π π r 2 = ( 2 + 1 ) 2 4
Therefore a + b + c = 4 + 2 + 1 = 7 .
Hi Mr Cheong, great solution. But how do we prove that the quarter circle radius line will definitely pass through the center of the inscribed circle?
Log in to reply
Wherever the circle touches a straight line or a circle of larger radius it does so tangentially. The normal or perpendicular to the tangent at the point of contact always passes through the center of the circle. The radius to any point on the circumference is always perpendicular to the tangent at that point. This is the property of circle.
Radius of the quarter circle = R
Radius of full circle = r
( R − r ) 2 = 2 r 2
⟹ R = r ( 2 + 1 )
⟹ the required ratio of areas is
4 ( R r ) 2 = ( 2 + 1 ) 2 4
So a = 4 , b = 2 , c = 1 , a + b + c = 7 .