Who's In-volute?
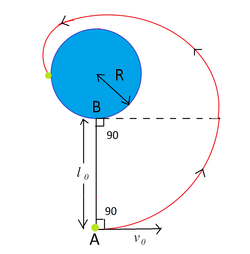 A horizontal plane supports a fixed vertical cylinder of radius
and a ball
attached to the cylinder by a horizontal thread
of length
. An initial velocity
is imparted to the ball as shown in the figure. The coefficient of restitution is
. Find the time in which the velocity of the ball reduces to
.
A horizontal plane supports a fixed vertical cylinder of radius
and a ball
attached to the cylinder by a horizontal thread
of length
. An initial velocity
is imparted to the ball as shown in the figure. The coefficient of restitution is
. Find the time in which the velocity of the ball reduces to
.
There is no friction between the ball and the plane. Round off the answer to the closest integer.
This is my first original problem on Brilliant. Please guide me if I haven't been able to follow the guidelines properly. :)
The answer is 107.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Here, e = u b a l l − u c y l i n d e r v c y l i n d e r − v b a l l
= u b a l l − 0 0 − v b a l l
Thus after each collision v b a l l = − e u b a l l Thus, after n collisions, ∣ v ∣ = e n u 0 .
The speed of the ball is not affected by the string because the string always exerts a force which is normal to the ball's velocity.
It can also be found out that the length of the involute path is 2 R l 0 2 = a
and the length of the Quarter circle is 2 π l 0 = b
For the first collision the ball travels a + b and for all the successive collisions it travels 2 ( a + b ) .
Total time for the velocity to be reduced to n v 0 = v 0 a + b + e v 0 2 ( a + b ) + e 2 v 0 2 ( a + b ) . . . . e n − 1 v 0 2 ( a + b )
T = v 0 a + b + e v 0 2 ( a + b ) ( e 1 − 1 ( e 1 ) n − 1 − 1 )
As final velocity has to be 1 6 v 0 the ball must collide 8 times i n a l l . Thus n = 8 .
On substituting the values of l 0 , v 0 , R , n and e we get T = 1 0 7 . 1 s which can be rounded off to 1 0 7 s