Who's up to the challenge? 4

$\begin{aligned} \int_0^1 \frac{x\sin x \cos x}{e^x} dx & = \int_0^1 \frac{x\sin (2x)}{2e^x} dx \\ & = \frac{i}{4} \int_0^1x e^{-x} \left( e^{-2xi}-e^{2xi} \right) dx \\ & = \frac{i}{4} \int_0^1x \left( e^{-(1+2i)x}-e^{-(1-2i)x} \right) dx \\ & = \frac{i}{4} \int_0^1 x \left( e^{-(1+2i)\color{#3D99F6}{a}x}-e^{-(1-2i)\color{#3D99F6}{a}x} \right) dx \quad \quad \small \color{#3D99F6}{\text{where }a=1} \\ & = \frac{i}{4} \int_0^1 \color{#3D99F6}{\frac{\partial}{\partial a}} \left(- \frac{e^{-(1+2i)\color{#3D99F6}{a}x}}{\color{#3D99F6}{1+2i}} + \frac{e^{-(1-2i)\color{#3D99F6}{a}x}}{\color{#3D99F6}{1-2i}} \right) dx \\ & = \frac{i}{4} \times \frac{\partial}{\partial a} \int_0^1 \left(-\frac{e^{-(1+2i)ax}}{1+2i} + \frac{e^{-(1-2i)ax}}{1-2i} \right) dx \\ & = \frac{i}{4} \times \frac{\partial}{\partial a} \left[\frac{e^{-(1+2i)ax}}{a(1+2i)^2} - \frac{e^{-(1-2i)ax}}{a(1-2i)^2} \right]_0^1 \\ & = \frac{i}{4} \times \frac{\partial}{\partial a} \left(\frac{e^{-(1+2i)a}-1}{a(-3+4i)} - \frac{e^{-(1-2i)a}-1}{a(-3-4i)} \right) \\ & = -\frac{i}{4} \times \frac{\partial}{\partial a} \left(\frac{e^{-(1+2i)a}-1}{a(3-4i)} - \frac{e^{-(1-2i)a}-1}{a(3+4i)} \right) \\ & = \small - \frac{i}{4} \left(-\frac{e^{-(1+2i)a}-1}{a^2(3-4i)} - \frac{(1+2i) e^{-(1+2i)a}}{a(3-4i)} + \frac{e^{-(1-2i)a}-1}{a^2(3+4i)} + \frac{(1-2i)e^{-(1-2i)a}}{a(3+4i)} \right) \\ & = \small - \frac{i}{4} \left(\frac{1-2(1+i) e^{-(1+2i)}}{3-4i} + \frac{2(1-i)e^{-(1-2i)}-1}{3+4i} \right) \quad \quad \color{#3D99F6}{\text{Putting }a=1} \\ & = \small - \frac{i}{4} \left(\frac{8i-2(3+4i)(1+i)e^{-(1+2i)}+2(3-4i)(1-i)e^{-(1-2i)}}{25} \right) \\ & = \small - \frac{i}{25} \left(2i + \frac{(1-7i)e^{-(1+2i)}-(1+7i)e^{-(1-2i)}}{2} \right) \\ & = \small - \frac{i}{25} \left(2i + \frac{e^{-1}\left(e^{-2i}-e^{2i} -7ie^{-2i}-7ie^{2i} \right)}{2} \right) \\ & = - \frac{-2e+\sin(2)+7\cos(2)}{25e} \end{aligned}$

$\Rightarrow A+B+C+D+F = 2+2+7+2+25 = \boxed{38}$

Let $\Large 2I(a) = \int_{0}^{1} e^{ax}sin(2x) dx$ So $\Large 2I'(a) = \int_{0}^{1} xe^{ax}sin(2x) dx$ So we need $I'(-1)$ . Using the standard integral

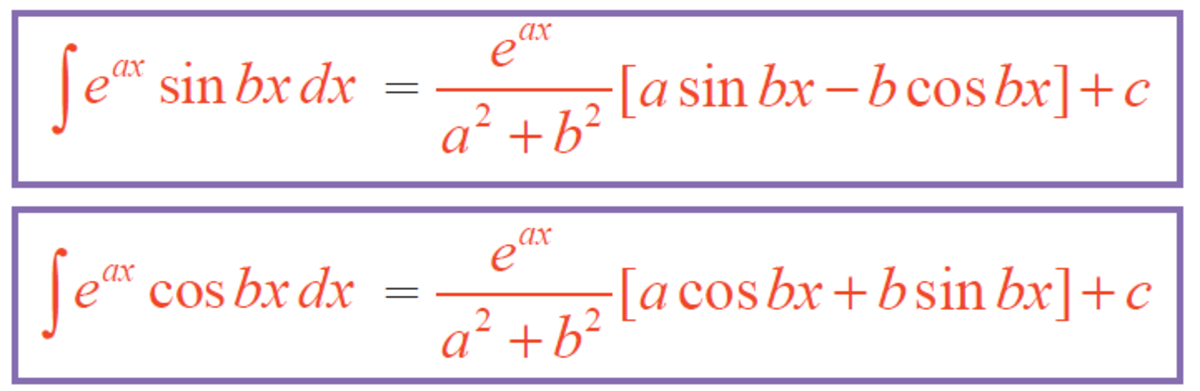
We have :-

$\Large 2I(a) = \frac{e^{a}(asin(2)-2cos2)}{a^{2}+4} + \frac{2}{a^{2}+4}$

differentiating both sides wrt $a$ we have:- $\Large 2I'(a) = \frac{e^{a}(asin(2) - 2cos(2) + sin(2)}{a^{2}+4} - \frac{2ae^{a}(asin(2) - 2cos(2))}{(a^{2} + 4)^{2}} -\frac{4a}{(a^{2} + 4)^{2}}$

Substitute $a = -1$ to get

$\Large I'(-1) = -\frac{-2e+sin(2) + 7cos(2)}{25e}$

So our answer is $38$