Why auroras happen at the poles

A magnetic field can rotate the direction of the velocity of an isolated charged particle but cannot alter the magnitude. This is because the magnetic field can only apply force that is perpendicular to the path of the particle. It follows that a magnetic field can do no work on an isolated charge. We can see this in our case by applying the right hand rule:

With the velocity $\vec{v}$ coming out of the page, and the magnetic field pointing along the radial vector, their cross product makes a vector that points up and towards the $z$ -axis, as indicated by the green vector in the diagram above. In effect, the field at the North pole cannot move the charged particle from the line that's generated by extending the radial vector because such a movement would change $r$ without changing the velocity, leading to an increase in the energy of the system, meaning that the magnetic field performed some work on the particle. The particle must therefore stay on the surface of the cone, that's generated by revolving the radial vector about the $z$ -axis, as the problem claims.

Rotating in a curved path gives rise to a centrifugal acceleration, shown as the blue arrow in the diagram below: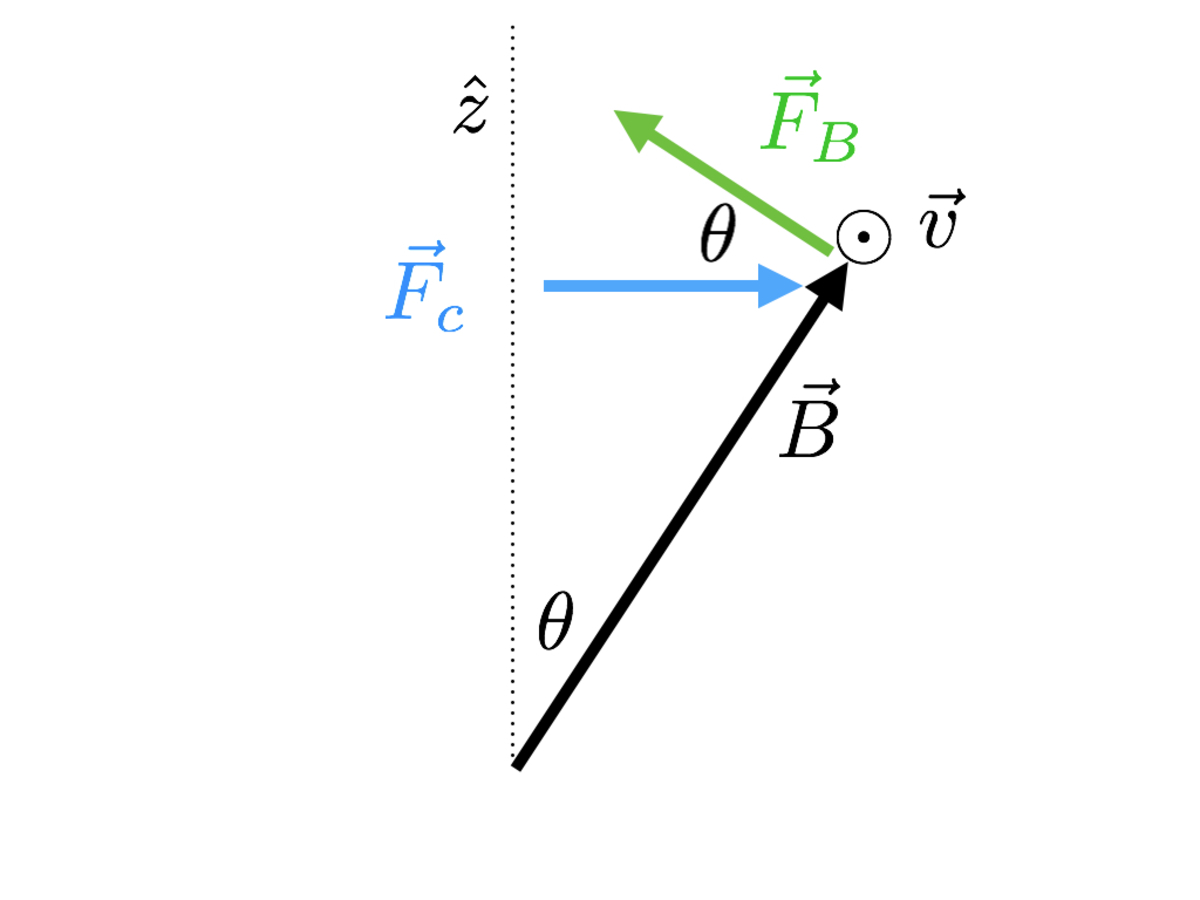

Were the magnetic field in this problem a vertical one, the centrifugal force could be balanced perfectly by the Lorentz force, leading to a circular path. However we've shown that the magnetic field at the pole keeps the charged particle on the conical surface, therefore the Lorentz force only balances the component of the centrifugal force that's projected along the direction of the Lorentz force:

Putting this in concrete terms, the component of the centrifugal acceleration vector $\vec{F}_c$ along the direction of the Lorentz force is $F_c\cos\theta$ .

The centrifugal acceleration is given by the usual form $\displaystyle\frac{v^2}{r'}$ .

However, we're given the straight line distance from the particle to the pole, not the perpendicular distance, therefore $\displaystyle r' = r\sin\theta$ and the centrifugal acceleration is $\displaystyle a_c = \frac{F_c}{m} = \frac{v^2}{r\sin\theta}$ .

Altogether, the component of the centrifugal acceleration that's along the direction of the Lorentz force is given by $\displaystyle a_c\cos\theta=\frac{v^2}{r}\frac{\cos\theta}{\sin\theta}$ .

Now, the Lorentz acceleration is given by $\displaystyle \frac{F_B}{m}=\frac{q}{m}\vec{v}\times\vec{B} = \frac{qvk}{mr^2}$ .

Equating this with the component of the centrifugal acceleration perpendicular to the surface, we have:

$\begin{aligned} \frac{v^2}{r}\frac{\cos\theta}{\sin\theta} &= \frac{qvk}{mr^2} \\ \tan\theta &= \frac{mrv}{kq} \end{aligned}$

or

$\boxed{\displaystyle \theta = \tan^{-1}\left(\frac{mrv}{kq}\right)}$

Using the parameters provided, we have $\displaystyle\theta = \tan^{-1} \frac{5\times 1\times 2}{3\times 4} = \tan^{-1}\frac56 \approx 40^{\circ}$ .

Let the monopole be at the origin $(0,0,0)$ , the charge at $(0,r,0)$ with a velocity of $(v,0,0)$ at the start. The force is $(0,0,(qvk)/r^2)$ , and hence acceleration is $(0,0,(qvk)/(mr^2))$ . At time = dt, the velocity of the charge will be $(v,0,(qvkdt)/(mr^2))$ and the average velocity of the charge in this time will be $(v,0,(qvkdt)/(2mr^2))$ . Hence the position at time = dt will be $(vdt,r,(qvkdt^2)/(2mr^2))$ . The distance from the origin approximates to $r+v^2dt^2/2$ .

Hence points $B: (vdt,r,(qvkdt^2)/(2mr^2))$ and $A: (0,r+v^2dt^2/2 ,0)$ are both on the cone the charge moves on and equidistant from the origin. By symmetry, $C: (-vdt,r,(qvkdt^2)/(2mr^2))$ is also on the cone and equidistant from the origin.

The circumradius of isosceles triangle $ABC$ is given by $R= AB^2/(4AB^2-BC^2)^{0.5}$ . This is easily provable using similar triangles which I shall not show here due to a lack of diagrams. Using Pythagoras theorem, $AB^2 = v^2dt^2 + ((qvkdt^2)/(2mr^2))^2$ $BC^2=4v^2dt^2$ . Substituting the above into the equation for $R$ , we have $R = 1/(1+((qk)/(mvr^2))^2)^{0.5}$ . The angle of the cone is $arcsin(R/(r+v^2dt^2/2) \approx arcsin(R/r) = 39.8 degrees$ .

We have: $m\overrightarrow{dv}=\overrightarrow{F}dt=q\overrightarrow{v} \times \overrightarrow{B} dt=q\overrightarrow{dr} \times \overrightarrow{B}$

Therefore, $\overrightarrow{r} \times \overrightarrow{dv}=\frac{q}{m} \overrightarrow{r} \times (\overrightarrow{dr} \times \overrightarrow{B})$ .

Since $\overrightarrow{B}=\frac{k\overrightarrow{r}}{r^3}$ , we have:

$\overrightarrow{r} \times \overrightarrow{dv}=\frac{qk}{mr^3} \overrightarrow{r} \times (\overrightarrow{dr} \times \overrightarrow{r})$

$=\frac{qk}{mr^3} [(\overrightarrow{r}.\overrightarrow{r})\overrightarrow{dr}- (\overrightarrow{r}.\overrightarrow{dr})\overrightarrow{r})]$ .

Since $\overrightarrow{r}.\overrightarrow{r}=r^2$ and $\overrightarrow{r}.\overrightarrow{dr}=d(\overrightarrow{r}^2)=d(r^2)=rdr$ , we have:

$\overrightarrow{r} \times \overrightarrow{dv}=\frac{qk}{mr^3} (r^2\overrightarrow{dr}- rdr\overrightarrow{r})$

$=\frac{qk}{m} (\frac{\overrightarrow{dr}}{r}-\frac{dr\overrightarrow{r}}{r^2})$

$=\frac{qk}{m} d(\frac{\overrightarrow{r}}{r})$ .

We also have: $d(\overrightarrow{r} \times \overrightarrow{v})=\overrightarrow{dr} \times \overrightarrow{v}+\overrightarrow{r} \times \overrightarrow{dv}$

$=dt \overrightarrow{v} \times \overrightarrow{v}+\overrightarrow{r} \times \overrightarrow{dv}=\overrightarrow{r} \times \overrightarrow{dv}$ .

Therefore, $\frac{qk}{m} d(\frac{\overrightarrow{r}}{r})=d(\overrightarrow{r} \times \overrightarrow{v})$ .

Therefore, $\frac{qk}{m} \frac{\overrightarrow{r}}{r}=\overrightarrow{r} \times \overrightarrow{v} + \overrightarrow{C}$ where $\overrightarrow{C}$ is a constant vector, as in the figure below.

image

We know that the magnitude of vectors $\frac{qk}{m} \frac{\overrightarrow{r}}{r}$ and $\overrightarrow{C}$ is constant and $\frac{qk}{m} \frac{\overrightarrow{r}}{r} \perp \overrightarrow{r} \times \overrightarrow{v}$ . Therefore, the magnitude of vector $\overrightarrow{r} \times \overrightarrow{v}$ is constant and the shape of the "triangle vector" is constant.

Therefore, angle $\theta$ between $\overrightarrow{r}$ and $\overrightarrow{C}$ is constant. This implies that the trajectory of the charge is on a cone with $\tan \theta = \frac{m|\overrightarrow{r} \times \overrightarrow{v}|}{qk}=\frac{mr_0v_0}{qk}$ .

Therefore, $\theta \approx 39.81^{\circ}$ .

Note that $\begin{array}{rcl} \tfrac{d}{dt}\hat{\mathbf{r}} & = & \tfrac{d}{dt}(r^{-1}\mathbf{r}) \; = \; r^{-1}\dot{\mathbf{r}} - r^{-2}\dot{r}\mathbf{r} \\ & = & r^{-1}\dot{\mathbf{r}} - r^{-3}(\mathbf{r}\cdot\dot{\mathbf{r}})\mathbf{r} \; = \; r^{-3}\big[(\mathbf{r}\cdot\mathbf{r})\dot{\mathbf{r}} - (\mathbf{r}\cdot\dot{\mathbf{r}})\mathbf{r}\big] \\ & = & r^{-3}\mathbf{r} \wedge (\dot{\mathbf{r}} \wedge \mathbf{r}) \end{array}$ Since the equation of motion for the charged particle is $m\ddot{\mathbf{r}} \; = \; q\dot{\mathbf{r}} \wedge \mathbf{B} \; = \; \tfrac{qk}{r^3}\dot{\mathbf{r}} \wedge \mathbf{r}$ we deduce that $qk\tfrac{d}{dt}\hat{\mathbf{r}} \; = \; m\mathbf{r} \wedge \ddot{\mathbf{r}} \; = \; m\tfrac{d}{dt}(\mathbf{r} \wedge \dot{\mathbf{r}})$ and so the vector $\mathbf{p} = qk\hat{\mathbf{r}} - m\mathbf{r}\wedge\dot{\mathbf{r}}$ is constant, and since $\mathbf{p}\cdot\mathbf{r} \; = \; qkr$ we deduce that the particle moves on a cone with axis pointing in the direction of the vector $\mathbf{p}$ , and with semi-vertical angle $\alpha$ , where $qk = p\cos\alpha$ .

Since the initial velocity is perpendicular to the initial radial vector, we deduce that $\cos\alpha \; = \; \frac{qk}{\sqrt{q^2k^2 + m^2r_0^2v_0^2}}$ where $r_0$ is the initial radial distance and $v_0$ is the initial speed. In our case, this gives $\alpha = 39.8^\circ$ .