Why do they intersect so much?
Probability
Level
5
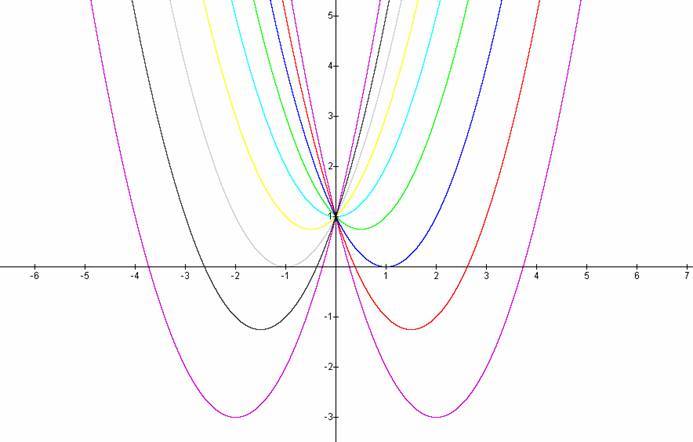 What is the maximum number of intersection points of 4 circles and 4 parabolas?
What is the maximum number of intersection points of 4 circles and 4 parabolas?
The answer is 100.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This is a very simple question.
It has three cases:
C a s e − I : Two circles cut each other.
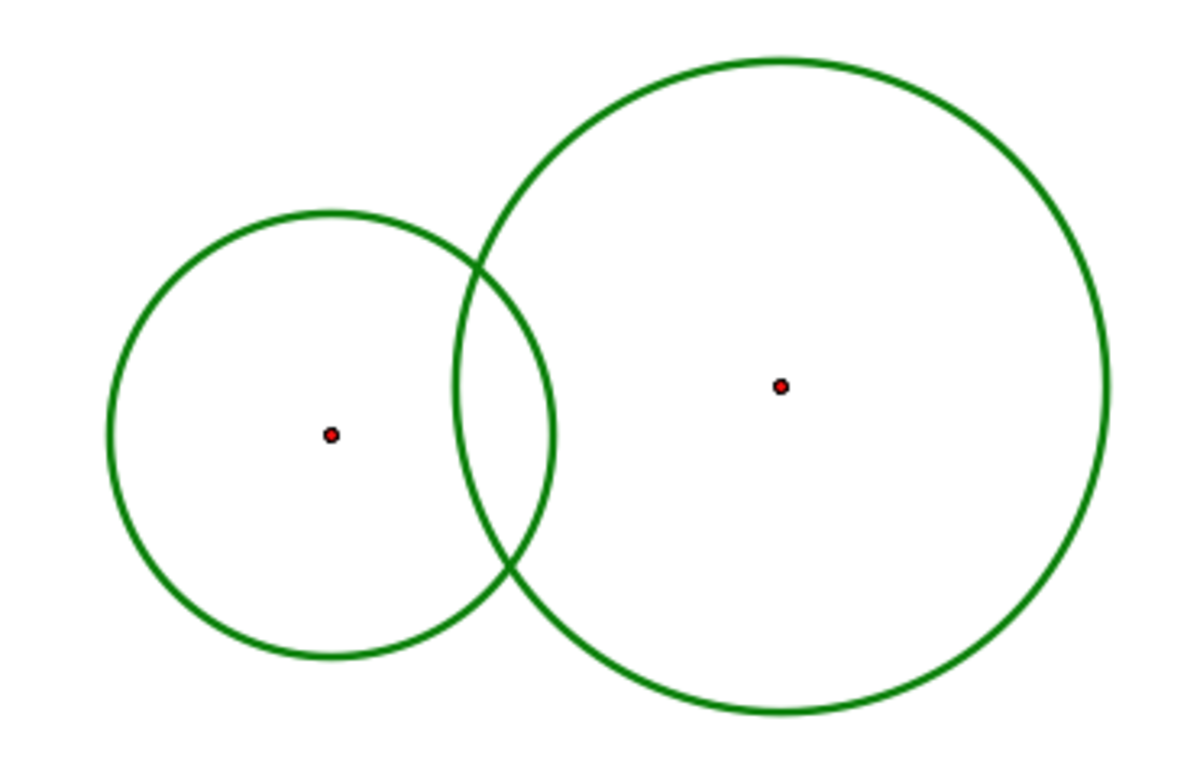 The maximum number of intersection points is 2 .
The maximum number of intersection points is 2 .
Therefore, ( 2 4 ) × 2 = 1 2 [ Since we have to select any two circles and then each such pair have two intersection points]
C a s e − I I : Two parabolas cut each other.
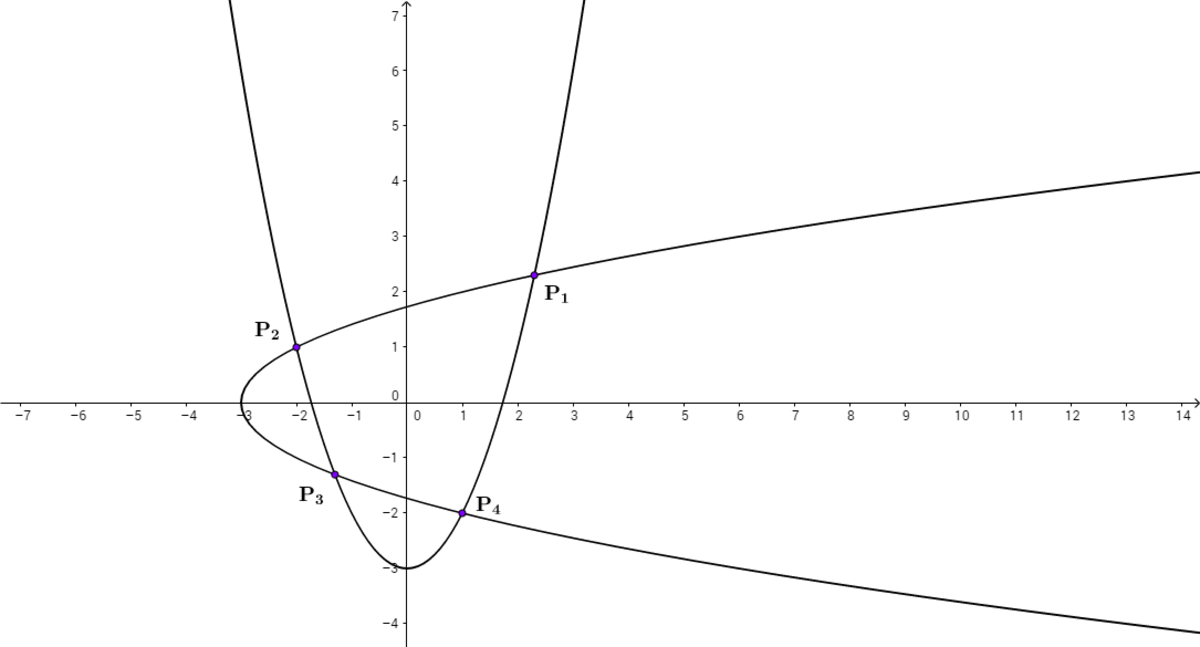 The maximum number of intersection points is 4 .
The maximum number of intersection points is 4 .
Therefore, ( 2 4 ) × 4 = 2 4 [ Since we have to select any two parabolas and then each such pair have four intersection points]
C a s e − I I I : One circle and on parabola cut each other.
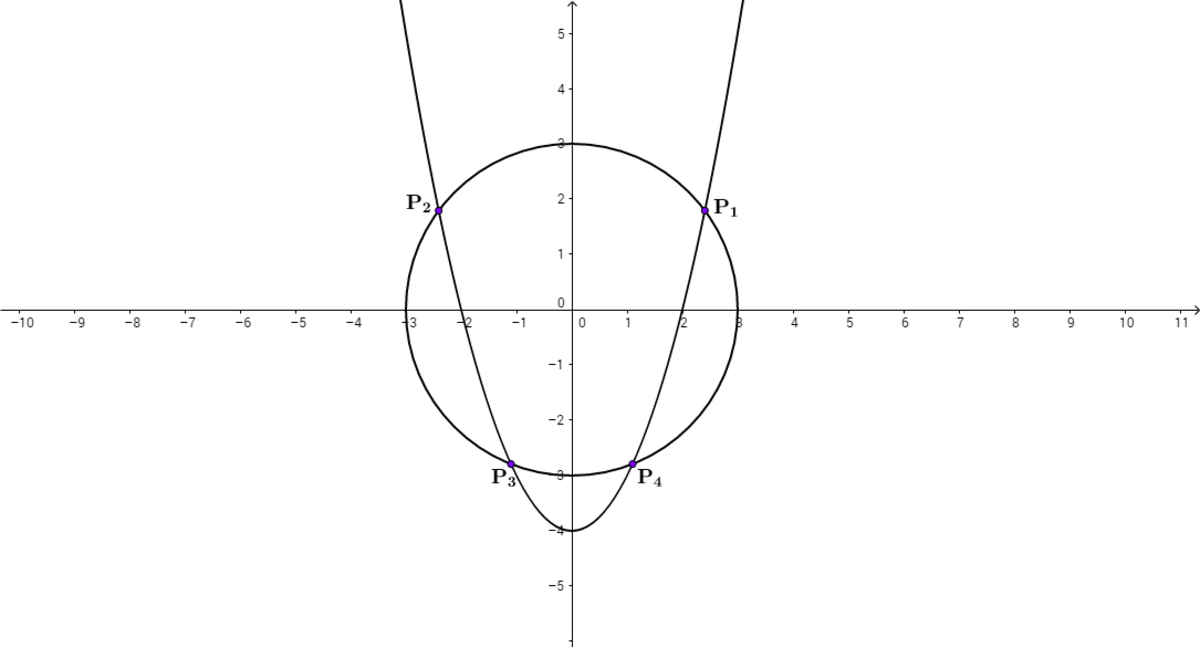 The maximum number of intersection points is 2 .
The maximum number of intersection points is 2 .
Therefore, ( 1 4 ) × ( 1 4 ) × 4 = 6 4 [ Since we have to select any one circle and one parabola and then each such pair have four intersection points]
Thus , total number of intersection points is 1 2 + 2 4 + 6 4 = 1 0 0