Why Does Ptolemy Start With :-P

Geometry Level 2

$ABCD$ is a cyclic quadrilateral with $\displaystyle \overline{AB}=11$ and $\displaystyle \overline{CD}=19$ . $P$ and $Q$ are points on $\overline{AB}$ and $\overline{CD}$ , respectively, such that $\displaystyle \overline{AP}=6$ , $\displaystyle \overline{DQ}=7$ , and $\displaystyle \overline{PQ}=27.$ Determine the length of the line segment formed when $\displaystyle \overline{PQ}$ is extended from both sides until it reaches the circle.

Note : The image is not drawn to scale.

The answer is 31.

3 solutions

Michael Ng
Jan 22, 2015

This is a nice problem! Let $PQ$ meet the circle creating the line $XPQY$ (where $X$ and $Y$ are the intersections with the circle). Let $PX = a$ and $QY = b$ for brevity. Then by intersecting chords, $a(27+b) = 6 \times 5 \\ b(27+a) =7 \times 12$ and solving these gives $a=1, b=3$ . Therefore the answer is $\boxed{31}$ .

Ha, I used the same solution, but I cut it short when I realized the answer is probably a positive integer. So 6*5 = 30 = 27a + ab, to which the only solution in the natural numbers is (a, b) = (1, 3). Finally 27 + a + b = 31

Caleb Townsend - 6 years, 4 months ago

@Satvik Golechha FYI, for images of geom diagrams, it is often better to use a thicker line, so that it can be easier to see.

Calvin Lin Staff - 6 years, 4 months ago

Thanks. Will keep that in mind next time. BTW A drawing tool on Brilliant would make things much easier... :D

Satvik Golechha - 6 years, 4 months ago

Noted. Thanks!

Calvin Lin Staff - 6 years, 4 months ago

I used coordinate geometry for that ,it was too long but I got the answer

Neelam Jangid - 3 years, 10 months ago

This is a nice transcendence example of Property of similar triangles and theorems on circular angles

Ritabrata Roy - 3 years, 1 month ago

I had reached those 2 equations, but how to solve them?

Subham pan - 1 year, 2 months ago

If you take their difference, you get $27 (b-a) = 54$ so $b - a = 2$ . Substitute that into either equation, and you get a quadratic for $a$ giving $a = 1, -30$ .

Calvin Lin Staff - 1 year, 2 months ago

A Former Brilliant Member
Oct 22, 2017

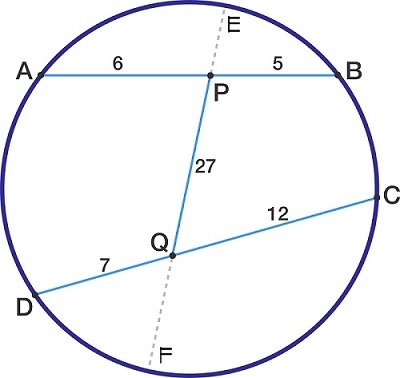By the power of a point , we have

$PE(PF)=PB(PA)=5(6)=30$

$PE(27+QF)=30$

$PE=\dfrac{30}{27+QF}$ $\color{#D61F06}(1)$

By the power of a point again, we have

$QF(QE)=7(12)=84$

$QF(27+PE)=84$ $\color{#D61F06}(2)$

Substitute $\color{#D61F06}(1)$ in $\color{#D61F06}(2)$ , we have

$QF\left(27+\dfrac{30}{27+QF}\right)=84$

$(QF)^2+25QF-84=0$

By factoring, we have

$(QF+28)(QF-3)=0$

$QF=-28$ or $QF=3$ (reject the negative value)

So, $QF=3$ .

It follows that,

$PE=\dfrac{30}{27+QF}=\dfrac{30}{27+3}=1$

Finally,

$EF=27+3+1=$ $\boxed{31}$

What is a power of the point?

Syio t - 2 years ago

That comes in coordinate geometry

Origin X - 1 year, 11 months ago

If a point is an intersection of two lines that joins 2 points each on the circumference of the circle, such that all four points are on the circumference , or they can become a cyclic quadrilateral. Let’s say a, b , c and d are points on circumference, and line ab and line cd intersect each other in circle and let’s call intersection point p. Theorem power of the point states that ap pb=cp pd. Or line ( from circumference to intersection )*(line from intersection to other end of line in circumference)=other line’s part from circumference to intersection) *(part of the line from intersection to other end of line in circumference).

Shreyas Murali - 8 months, 1 week ago

Long Hua
Jan 14, 2021

Why is this problem under "Ptolemy's Theorem"?

The same question I asked myself.

prashant sharma - 2 weeks, 5 days ago

Why Does Ptolemy Start With :-P

The answer is 31.

3 solutions

0 pending reports