Why does this number keep popping up everywhere?
A block of mass (block 1) remains at rest, when a block of mass (block 2) comes in with a velocity and collides against the block 1. This triggers a series of collisions. All the collisions are perfectly elastic, and there is no friction in the system.
Look at the diagram below:
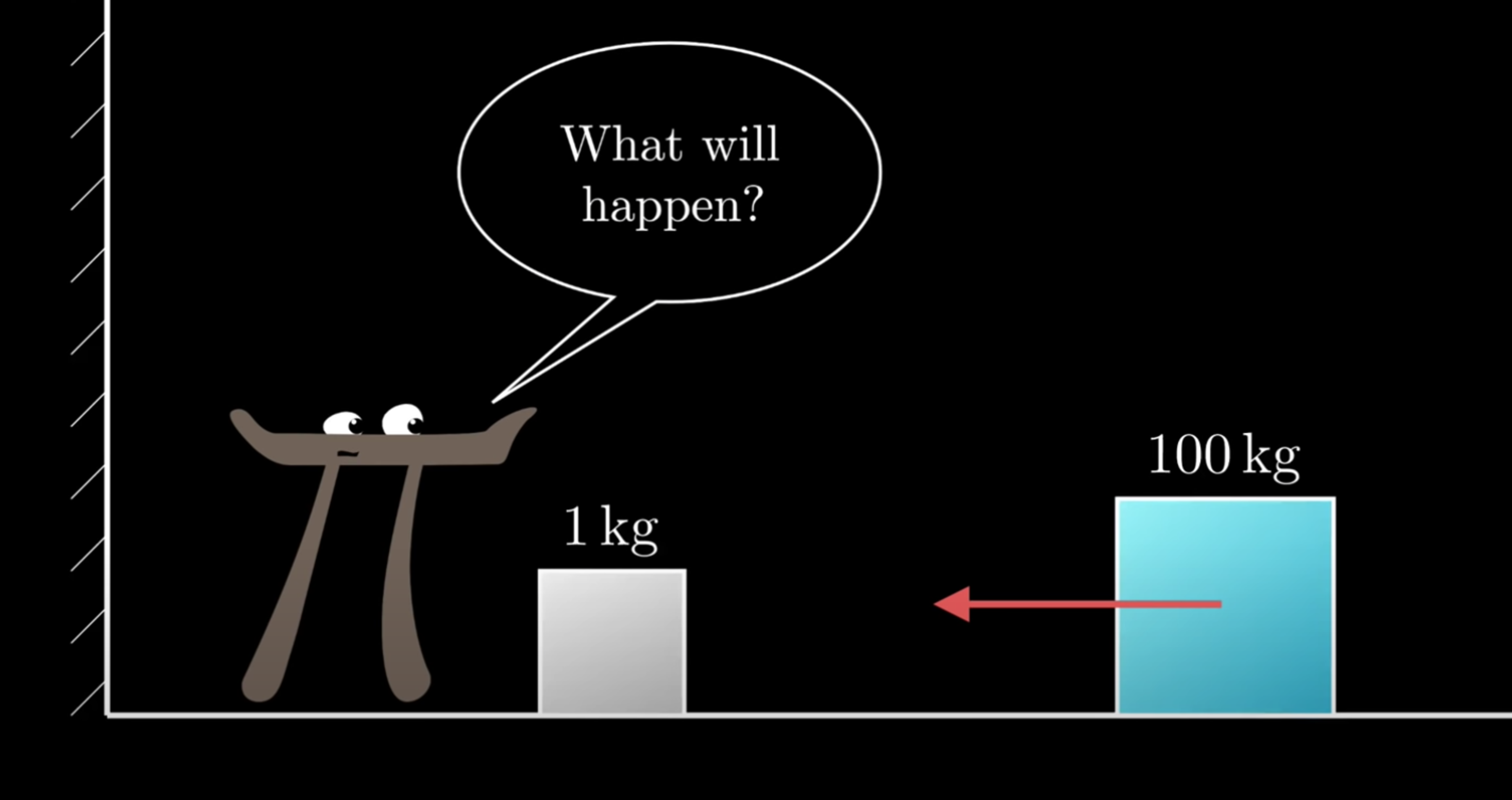
There is a wall behind block 1. The block deflects off of the wall with the exact same momentum as it came in with.
What are the maximum amount of collisions that occur before block 2 shoots off into infinity and before block 1 is left with no velocity to collide anymore? How many collisions occur in this system?
Divide the number of collisions that will occur by and select the result.
What is the significance of the answer?
I don't expect you to actually simulate the system; I made it multiple choice so you can just have a guess. The answer will surprise you very much.
Note: this is not an original problem. The problem and its solution was published in a paper in 1995 by mathematician Gregory Galperin.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
You can see the explanation by 3Blue1Brown here: Video link . In his solution, he states that if the mass of the heavier block is 1 0 0 ( d − 1 ) and the lighter block to 1, then the number of collisions will be the first d digits of pi.