Why don't you sketch the graph?
Which of the following functions, with domain D f = ( − ∞ , ∞ ) will have a graph which is a n-shaped parabola (it has a maximum point) with no y -intercept?
Details: It may or may not have x -intercepts.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Now, for a function to have a parabola graph, it must be a quadratic function.
Therefore, f ( x ) = x 3 − 3 x + 5 and f ( x ) = 3 x + 9 do not satisfy the conditions.
Next, the graph is a n-shaped parabola, which is something like this:
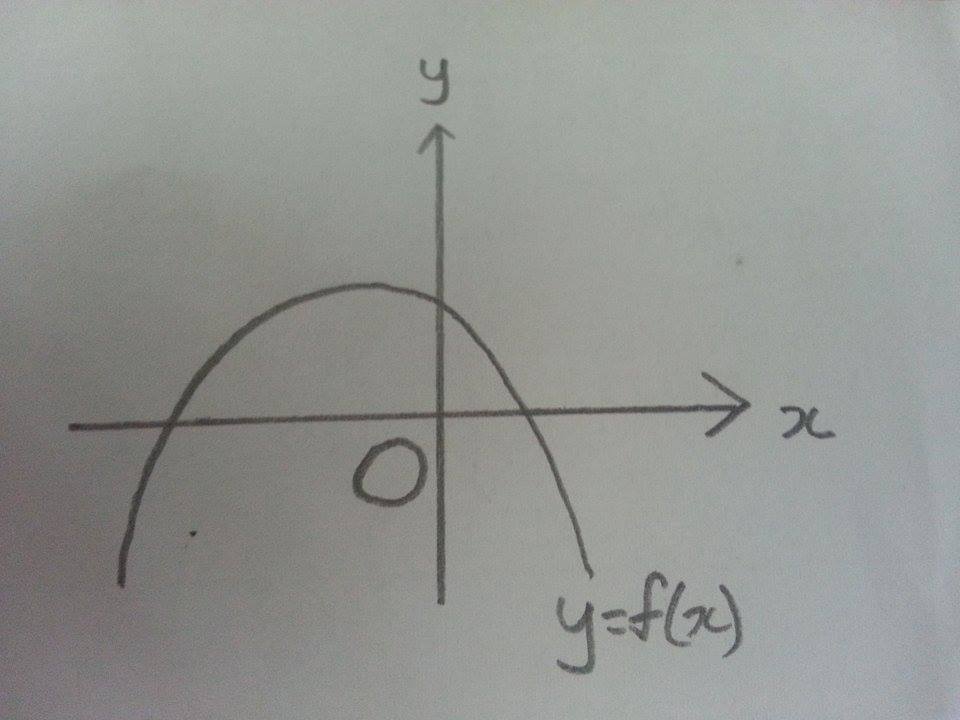
For quadratic functions f ( x ) = a x 2 + b x + c , a = 0 to have this kind of graph, the coefficient of x 2 must be negative, which is a < 0
Two of the choices satisfies this: f ( x ) = − x 2 − 5 x − 9 and f ( x ) = − 3 x 2 − 2 x + 4
The final condition: The graph has no y -intercept.
Sadly, none of the two choices satisfy this. As long as the domain is defined as D f = ( − ∞ , ∞ ) , it will pass through the y -axis, and there will be a y -intercept.
Therefore, None of the functions given are correct
It is simpler to evaluate f(0).
No y-intercept means at x=0, y has no real value for given condition .
As can be seen, for each function, Df =(−∞,∞) and NO y-intercept , when x=0, y does have a real value.
So no function satisfy this condition.