Is the integral actually zero?
The following shows a portion of the graph for f ( x ) = 1 − tan 2 x , in which all regions bound by the x -axis and f ( x ) are shaded.
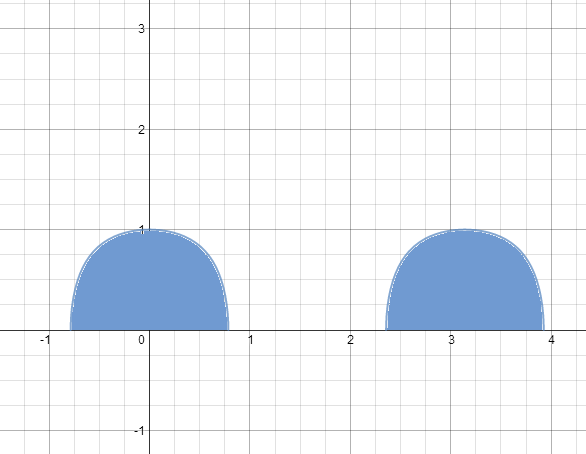
Considering the periodic properties of f ( x ) , the area of any shaded region can be expressed in the form π tan A π , with A being a positive, root-free integer. Find A .
This problem is original. The picture of the graph was produced from Desmos .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Same here, Sir! (+1). Only one small correction, the integral
∫ 0 ∞ 2 t 2 + 1 2 d t
is actually:
2 tan − 1 2 t
Log in to reply
Correct your denominator first.
Thanks. I have changed it.
Log in to reply
I don't check usually.
We note that f ( x ) = 1 − tan 2 x is even; and that f ( 0 ) = 1 and f ( ± 4 π ) = 0 . Therefore, the area of the shaded region is given by:
I = ∫ − 4 π 4 π 1 − tan 2 x d x = 2 ∫ 0 4 π 1 − tan 2 x d x = 2 ∫ 0 1 u 2 + 1 1 − u 2 d u = 2 ∫ 0 2 π sin 2 θ + 1 cos 2 θ d θ = 2 ∫ 0 2 π tan 2 θ + sec 2 θ 1 d θ = 2 ∫ 0 2 π 2 tan 2 θ + 1 1 d θ = 2 ∫ 0 ∞ ( 2 t 2 + 1 ) ( t 2 + 1 ) 1 d t = 2 ∫ 0 ∞ ( 2 t 2 + 1 2 − t 2 + 1 1 ) d t = 2 [ 2 tan − 1 2 t − tan − 1 t ] 0 ∞ = ( 2 − 1 ) π = π tan 8 π Since the integral is even. Let u = tan x ⟹ d u = sec 2 x d x Let u = sin θ ⟹ d u = cos θ d θ Let t = tan θ ⟹ d t = sec 2 θ d θ
⟹ A = 8