Why Isn't It Reducible?
Let A = 2 1 × 4 3 × 6 5 × ⋯ × 2 0 1 4 2 0 1 3 B = 3 2 × 5 4 × 7 6 × ⋯ × 2 0 1 3 2 0 1 2 C = 2 0 1 4 1
Which of the following statements is true?
1
.
A
<
B
<
C
2
.
A
<
C
<
B
3
.
B
<
A
<
C
4
.
B
<
C
<
A
5
.
C
<
A
<
B
6
.
C
<
B
<
A
7
.
Two of them are equal
8
.
All of them are equal
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
32 solutions
Well done sir ! This is an ultimate approach !
Log in to reply
thanks Priyansh.
Same question in A.I Prelipiko.
This is so simple, I don't realize it
Yeah I did the same proof.
wow, great idea :)
did just the same.....:-)
I did it for a really small case, namely 1/2 * 3/4, vs 2/3, vs 1/sqrt(4)=1/2. then I just put that and assumed it was right... but yeah your solution is actually rigorous =)
Wonderful Just amazing Sir you are a
 Genius
Genius
Beautiful, simple, straightforward approach . Up Voted.
Very easy explanation. Thanks for that, helps a lot.
A good approach to the problem...
excellent sir? r u a student or teacher
Log in to reply
He's just everything... We're so proud to be his students.... @Chandra Shekhar Agrawal ... amazing teacher @Piyushkumar Palan
Correctly said @Aditya Raut .....proud to be his students.....
Log in to reply
The most upvoted solution I have seen, it has 96 upvotes including mine, just need 4 more to get a solid 1 0 0 .
superb!!! I was stuck after finding out the relation. it didn't clicked me what I was looking was a GM . Thanks!
just did the same here
Look at the form of A and B.Does it tell us that last term that is 2014 has any another property that is not owned by 4............Isn't it?So why not we try to obtain answer by taking last term as 4.............Nice naa.
Exactly the same proof! If I would have more experience in GP, this could be solved much faster!
Yeah, did the same. But the problem startled me for once.
I got both facts but couldn't summarise to get that it might be g.p.. Really u did excellent observation
Excellent observation
upvoted . A very good solution
Did just same &i got☺
Did the same way
Did the same!
Same method and nice problem :)
Elegant..nice .. Easy ty sir
Beautiful solution sir +1! Nice question also.!
Did the same !(+1)
Did the same! Nice! Easy peasy!
Multiply A and B to get:
A B = 2 0 1 4 1 ( ∗ ) .
Now divide A and B to get:
B A = 4 3 × 1 6 1 5 × 3 6 3 5 ⋯ 2 0 1 2 × 2 0 1 4 2 0 1 3 2
It is easy to see that the right hand side is less than 1, hence A < B ( ∗ ∗ ) .
Lets get back to ( ∗ ) , it is equal to C 2 . This shows that A , C and B are in geometric progression so the possible orders are: A < C < B and B < C < A but from ( ∗ ∗ ) , the only possible order is A < C < B .
A cool way to check wether A or B is bigger. Just one thing: B A = 4 3 × 1 6 1 5 × 3 6 3 5 × . . . × 2 0 1 2 2 2 0 1 1 × 2 0 1 3 × 2 0 1 4 2 0 1 3
Log in to reply
Nice one, didn't think about that. XD
Thanks! :)
All corresponding terms of A are less than those of B. B has one less term, & all terms are fractions. Therefore A<B. Isn't this better reasoning sir ?
Log in to reply
Yeah there was another person who did this way
I really think THERE MUST BE A MINIMUM of more than 3 options in such problems WHERE we get 3 attempts...
Okay, I don't get how A , B , C are in a geometric progression. Why and how?
Wrong.Check your proof.
Wrong proof. Lucky guy to get it right.
Wrong proof
Simple and Effective. The best of every answers. I thought in a variation of this way.
Log in to reply
You're wrong when you say that A/C=C/B=1/sqrt(2014) Even worse, you don't know how to use Latex...
Looks like I'm the only idiot who used Stirling's approximation to solve this one (sigh).
A= ( 2 n − 1 ) ! ! ) 2 n ! ! = π n 1 (simplified using Stirling's approximation) and B= 2 n × A 1 , where n = 2 2 0 1 4 = 1 0 0 7 .
Substitute n=1007 and you get:
A = 0.017779...
B = 0.27927...
C = 0.2228...
Clearly, B>C>A.
I guess as soon as I saw double factorials and a square root in the question, I jumped to Stirling's approximation. Doh!
Don't feel sad. Instead you are one of the geniuses since you have found a totally brand new method to solve. Furthermore there are such who weren't able to even solve it, keep up and always post novel solution no matter how complex they are because what may be complex to you might be beautiful to somebody else. Nice solution upvoted!
2
1
<
3
2
,
4
3
<
5
4
......
A has 1007 such terms while B has 1006 such terms.
thus B>A.
A
B
=C.
by AM GM inequality A+B>2C.
Thus B>C.
if A>C then then AB=
C
2
is not possible.
thus A<C<B
there is a problem in ur answer that is "if A>C then then AB=C^2 is not possible. thus A<C<B" it is possible to have A>C
Exactly As Satya said there is a flaw in your argument to deduce A < C. There can be cases where A>C and still satisfy A B = C
Log in to reply
can you elucidate such a case? keep in mind B>A and A,B and C are positive.
So, all of us have solved this amazing problem with our precious Number Theory knowledge.
But a great alternative came across my neurons. Its Programming , which would take around 5 milli seconds to calculate these big calculations!
So, here's my different C programmed Solution .
Source Code: _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
# i n c l u d e < s t d i o . h >
# i n c l u d e < m a t h . h >
int main()
{
double n=2,A=1;
printf("I am not a brilliant Mathematician.\nBut I have my programming knowledge and my great computer!\nSo it makes everything easy!");
while(n<2015){
A=A*((n-1)/n);
n=n+2;
}
printf("\n\nA=%.100lf",A);
double N=3,B=1;
while(N<2014){
B=B*((n-1)/n);
N=N+2;
}
printf("\n\nB=%.100lf",B);
printf("\n\nC=%.100lf\n\nSo, obviously\n1. B ia greater than C,\n2. C is greater than A.\n\n To express mathematically, A<C<B!!!",(1/sqrt(2014)));
return 0;
}
*Output: *
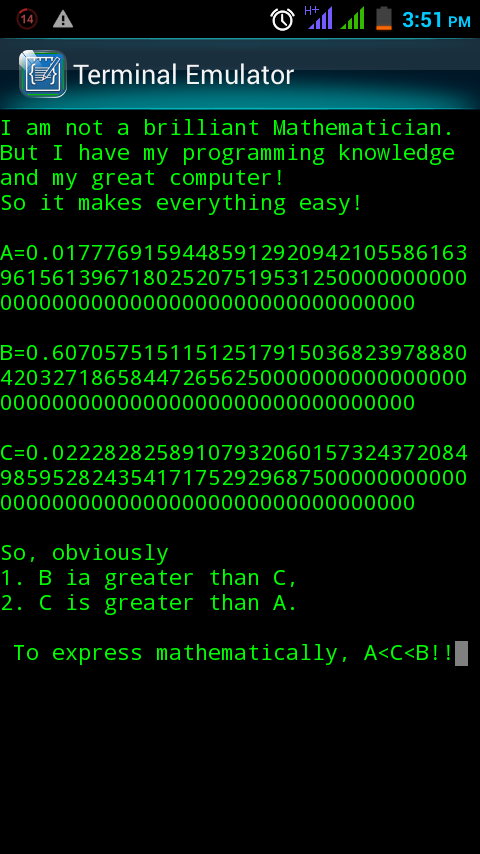
There's always thousands of ways to solve any mathematical Problem, right!!!
Right, but actually you've got the value of B wrong it is really: 0 . 0 2 7 9 3 0 8
0 . 0 2 7 9 3 0 8 4 7 5 7 9 6 5 2 4 2 2 to be a bit more precise. Or i = 1 ∏ 1 0 0 6 2 i + 1 2 i .
First note that: A × B = 2 0 1 4 1
Since A and B are rational numbers, neither A nor B can equal C. Also, since A times B equals C times C, we know that C is between A and B.
We can write A and B as: A = ( 2 1 × 4 3 × 6 5 × . . . × 2 0 1 2 2 0 1 1 ) × 2 0 1 4 2 0 1 3 B = ( 3 2 × 5 4 × 7 6 × . . . × 2 0 1 3 2 0 1 2 )
Note that for each fraction that is a factor of A, the corresponding fraction that is a factor of B is larger. Finally, the extra term that is a factor of A, (2013/2014), is less than 1. Therefore, A is less than B, so B > C > A .
notist that A=2013!!/2014!! multiply it by 2014!!/2014!! A=2014!/(2014!!)²=2014!/(1007! 1007! 2^2014)=(2014C1007)/2^2014 Same B=2012!!/2013!! 2012!!/2012!!= 2^2012 1006! 1006!/(2013 2012!) B=2^2012/(2013 (2012C1006)) so to compare A r B ,r is relation < or > (2014C1007)/2^2014 r 2^2012/(2013 (2012C1006)) i.e. 2014C1007 * 2013C1006 2013 r 2^2014 2^2012 as we know 2^2014=sum(2014Ck,k goes from 0 to 2014) so 2^2014 is at least 50 times bigger than 2014C1007,also 2^2012 is at least 50 times bigger than 2012C1006,so because 50 50/2013>1 that means that r is relation <,so A<B Similiar 1/√2014 < B because √2014 *2^2012 > 2013 2012C1006 because 50*√2014>2013 so C<B, also C>A because 2^2014> √2014 *2014C1007 beause 50>√2014 so A<C<B is correct
First we try A × B we get 2 1 × 3 2 × . . . × 2 0 1 3 2 0 1 2 × 2 0 1 4 2 0 1 3 .
A × B = 2 0 1 4 1
If A = B , then A = B = 2 0 1 4 1 = C
But A = B , then A > C > B or A < C < B (2 choices left, yay!)
Consider A and B ;
There're 1007 terms in A but there're only 1006 terms in B . (Don't think that A > B immediately.)
The problem of A is... A has 2 1 , which reduces a lot. (compare 4 3 of A to 3 2 of B , and so on... that doesn't change that much.)
Therefore, B > C > A (or A < C < B )... 2 ~~~
Note: A = B because the numerator and denominator of A and B are not the same.
Well your argument could be cleaned up a lot easier. Note that
2 1 < 3 2 , 4 3 < 5 4 and so on, and then A has another term less than 1 which reduces it even further, so we can definitely say that A < B
Your whole A has one more term argument is pretty irrelevant and makes it even more confusing than it has to be: If A has one term, that actually should suggest that A < B since each term is less than 1 , no?
Log in to reply
Yeah, that's true. My brain thinks that 2 0 1 4 2 0 1 3 is a big number. I'm going to kill my brain in 1 day. XP
I have also solved this, but your approach is much better. I failed to think this way, but I appreciate this! You kids are really more intelligent than us, though we are more experienced!!
Simple use mathematical induction for n=1 1 We get the answer in one step
first , if a and b are positive and a<b then b a < b + 1 a + 1 use the property to show than 2 1 < 3 2 , 4 3 < 5 4 .... 2 0 1 3 2 0 1 1 < 2 0 1 4 2 0 1 2 then by multiplying and considering that 2 0 1 4 2 0 1 3 < 1 we can find that A< B from AB=C we conclude that A<B<C.
note A*B=C^2
so A,B,C are in GM
so try 2,4,8
0.0177769159448591 0.0279308475796525 0.0222828258910793
A < C < B
- A x B = 1/2014 = C²
- so, A/C = C/B
- Hence either A<C<B or A>C>B
- Now, A = 0.5 x 0.75 x ......... 2007 numbers fraction and
- B = 0.66..7 x 0.80 x ...... 2006 numbers fraction.
- now, 0.5<0.6666...; 0.75<0.80 ...... up to 2006 numbers of terms.
- hence if we omit 2013/2014 i.e. the last fraction of A and say it is K, till then the product of fractions in K<B.
- also (2013/2014) <1, hence (2013/2014) x K is still less than B.
- Hence A<B
- so, A<C<B.
I wrote a mathlab script :-)
format long;
clear all;
A = 1;
B = 1;
C = 1/sqrt(2014);
for i = 1 : 1006
A = A*(2*i-1)/(2*i);
B = B*(2*i)/(2*i+1);
end
A = A*2013/2014;
A
B
C
Multiplying A and B gives us 1/2014, which is twice that of C. Therefore, if A and B were to be equal, then A, B, and C would all be the same.
However, if A or B was to be bigger than the other, we now have a situation where A<C<B or B<C<A. At this point, the answer is now narrowed down to 2, 4 or 8.
When looking at A and B, one may realize that every nth term in B is greater than the nth term of A, such as 1/2 < 2/3 for the first term, 3/4 < 4/5 and so on. Therefore, we can conclude B>A.
Using this information, the final answer seems to be B>C>A, or number 2. Which is right, by the way.
Right away, you can eliminate choice 8, because A and B are rational, while C is not.
Generalize it. Let n = number of terms in A. Then there are n-1 terms in B. And by looking at the cases, n=1, 2, 3, you can come to some quick conclusions (keep in mind that a vacuous product is =1). In the example shown, n=1007. Now if you "cycle" each of the numerators in A one place to the left, A becomes identical to 1/B, but with an extra factor of 1/2n = 1/2014 at the end. So:
2n·A·B = 2014·A·B = 1
C, however, is just 1/√(2n) = 1/√2014. Now you can also see that each term in A is < each term in B, with that extra 2013/2014 at the end of A. And since that extra term is < 1, it's clear that A < B (scratch 3, 4, 6, & 7).
But C² = 1/(2n) = 1/2014 = A·B. So C is the mean proportional of A & B, and that means:
A < C < B (choice #2)
1st step multiply A and B which gives AB=1/2014 In the 2nd step Square C which gives C^2= 1/2014 So, C^2= AB, that implies C is geometric mean of A and B....And also we know from 1st step A<B and as c is G.M, it follows the order A < B <C
just try it with first 2 terms of each A,B,C and u will get the answe.r
simple check for A= (1/2)*(3/4) b=2/3 c=1/square root of 4
this sequence is analogous to given compare values A=0.735 b=0.666 c=0.5 A<c<b
First thing I observed is
A*B = C^2
or, C is the geometric mean of A & B, it should lie between A and B
(NOTE: A,C,B being equal doesn't make sense as A and B are rational, C is irrational)
We have to figure out whether A<B or B<A
Now if we compare each terms of A & B:
1/2 is less than 2/3 .... 3/4 is less than 4/5 .... ... and so on ... 2011/2012 is less than 2012/2013
so: (1/2) (3/4) ...(2011/2012) < (2/3) (4/5) ...(2012/2013)
Now, 'A' is the LHS of the above inequality multiplied to (2013/2014) ... as (2013/2014) is a fraction, it reduces 'A' further.
So, A<B
and as, 'C' is lying between A &B
A<C<B
if u solve A & B, we arrive at B^2 = A*C therefore, A , B and C are in G.P. so, A<C<B
Sry, i made a mistake while typing,its c^2 = a*b
B > A is easy to derive by regular way of comparing fractions. By minute inspection of numerators and denominators, B > C and C > A can be derived. Hence the result.
A= product of (2n-1)/(2n) from 1 to 1006 * 2013/2014
B= product of (2n)/(2n+1) from 1 to 1006 * 1
comparing each term, we get A<B
A*B=1/2014
C is the geometric mean of A and B and must be in between
therefore A<C<B
Because every term in A is less than a corresponding term in B , we have that A < B . Also, we have that A B = 2 0 1 4 1 = C 2 , so C is the geometric mean of A and B , so A < C < B . Hence, the answer is 2 .
Clearly, A<B because 1/2 < 2/3 , 3/4 < 4/5 , and so on. Also, C is the geometric mean of A and B. So, A<C<B
We easily can see that AB = C 2
Also, A < B. So, A, C, B form an increasing G.P. Hence A < C < B.
We observe that A/B is almost 1/2014 < 1 so A<B.
Again, AB = C^2 so this implies C<B.
The hard part is to prove that A<C. For this I took the ratio A/C and as I calculated 1/2 x 3/4 x 5/6 x ... x 2013 / sqrt(2014) progressively I observed the product is decreasing (as it should be) and ultimately it falls off by 1/100 which on being multiplied with a two digit integer will definitely be < 1
For this question, there are some pointers that we can work with :
As each numerator of the fractions in A is present in the denominator of the fractions in B , except 2014. Hence, after cancellations, A B = 2 0 1 4 1 .
In addition, C 2 = 2 0 1 4 1 too.
Hence, A B = C 2 ---- Equation (1)
Now, consider each terms in A and B : 3 2 in B > 2 1 in A , 5 4 in B > 4 3 in A , ... until 2 0 1 3 2 0 1 2 in B > 2 0 1 2 2 0 1 1 in A . Note that the term 2 0 1 4 2 0 1 3 in A is not compared. With the following information :
As every term in B > its corresponding term in A except 2 0 1 4 2 0 1 3 .
Hence, B > A ′ , where A ′ denotes all the terms except 2 0 1 4 2 0 1 3 .
Now as 2 0 1 4 2 0 1 3 A ′ = A => A ′ > A . Hence , as B > A ′ > A , B > A
In addition, referring back to equation (1) , A B = C 2 , as the product of A and B yields the product of C and itself, hence, logically, C must lie between A and B for that to occur. Thus, as B > A , hence, B > C > A
Let A = a /(2014*b) B = b/a Use cross multiplication comparisons and result in B > C > A
A=1/2 3/4 ...2013/2014=3/2 5/4 ...2013/2012 1/2014=1/B 1/2014 Then AB=1/2014=C^2 It implies A<C<B or B<C<A B>1 then 1/B<1 also A=1/B*2014<1/2014<1 Hence A<C<B
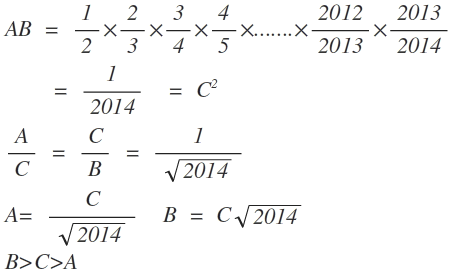
Let fractions in A be denoted as a 1 , a 2 , a 3 , . . . , a 1 0 0 7
Let fractions in B be denoted as b 1 , b 2 , b 3 , . . . , b 1 0 0 6
But a 1 < b 1 , a 2 < b 2 , a 3 < b 3 . . . . a 1 0 0 6 < b 1 0 0 6 , a 1 0 0 7 < 1
Multiplying all these, A < B
Observe that A × B = 2 0 1 4 1 = C 2
So A , C , B are positive numbers forming increasing G.P. (Geometric Progression)
Hence option 2 : A < C < B