Why not 2015?
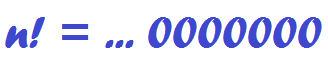 Find the sum of all positive integers
n
such that
n
!
ends with precisely
2
0
1
6
zeros.
Find the sum of all positive integers
n
such that
n
!
ends with precisely
2
0
1
6
zeros.
The answer is 40385.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Solved it the same way! Just wondering is there a better method for doing this so we get that n=8075 instead of getting 8066.5 right off the bat? Pls tell me
Log in to reply
Yes, we can use langrage's principle i.e., e p ( n ) = n − 1 n − S p ( n ) , where e p ( n ) is the highest power of p in n and S p ( n ) is the sum of the digits of n in base p .
Did it by the same way
The highest power of 5 thats contained in this number has to be the answer. Now with the number approaching 2016 that becomes a little imposing initially. What I did was some approximation to land close to the number As this is a sum of increasingly restrictive values, we are looking for a number which leads us close to the vicinity of 2016. Since this method focuses on the trial and error bit, thus a reasonable number to start with was 8000 as 8000/5 = 1600 and 8000/25 = 320 which together adds upto 1920 which gets us within reasonable proximity of 2016. A common technique, though not foolproof that I have observed which helps in such cases would be to focus on the numbers which are essentially multiples of 5(again not a fail safe method, it has glaring inadequacies). Proceeding this way we can arrive at 8075 with maybe 3-4 rounds of calculations.
Now, if any number n is chosen that has k zeroes at the end of n! then the next 4 numbers also will be ending with the same number of zeroes because its not until the next multiple of 5 does the number of zeroes change.
Any inputs are welcome
n=0
l=0
for i in range(0,10000,5):
l=i
n=0
while( l > 0):
n = n + l/5
l=l/5
if (n == 2016):
print 5*i+10
python code for the problem
To continue with this solution, I would like to say that this was a handy method for me.
We have to see no of 5's in the given number to be exactly 2016.
Let us consider a smaller number. For instance 5! = 5/5 = 1 which has only 1 0.
This continues but for 25! = 25/5 = 5/5 =1 which has 6 0's.
That is for multiple of 25,we will get a jump.
But for 125 = 125/5 = 25/5 =5/5 =1 has 31 0's.
We need to see the series 125,250,375,...
We know that 31(65) = 2015.
But 1250, 2500, 3250, 5000, 6250, 7500 each carries an extra 0 in them.
65th term = 125 + 64(125) = 65(125) = 8125 will have 8125/5 = 1625/5 =325/5 = 65/5 = 13/5 = 2 will have 2030 0's.
we get 8075 having 2016 0's if we check it.
The next 5 numbers will have exactly 2016 0's...8075...8079
Total is 40385.
To make a zero, we need the factors 2 and 5 . Since we will have more factors of 2 than 5 in any n ! calculation we need focus only on the factors of 5 .
Now in general there are x k = ⌊ k n ⌋ multiples of k less than or equal to n for any integer k . To find all the factors of 5 in n ! we will need to find
∑ m = 1 ∞ x 5 m , i.e., x 5 + x 2 5 + x 1 2 5 + . . . . . . .
We thus need to find all n such that this sum comes to 2 0 1 6 .
Next, note that for n = 3 1 2 5 this sum comes to 7 8 1 and for n = 1 5 6 2 5 this sum comes to 3 9 0 6 . So we are looking for values of n between these two values. Thus our sum will only involve a calculation of x 5 + x 2 5 + x 1 2 5 + x 6 2 5 + x 3 1 2 5 .
For a first estimate, look at the sum without the floor function, i.e.,
5 n + 2 5 n + 1 2 5 n + 6 2 5 n + 3 1 2 5 n = 2 0 1 6
⟹ 3 1 2 5 7 8 1 ∗ n = 2 0 1 6 ⟹ n = 8 0 6 6 . 5 8 . . .
As the least n we are looking for will be a multiple of 5 , we will need to make the sum calculations for multiples of 5 near to this initial estimate. For n = 8 0 7 0 we get a sum of 2 0 1 4 , and for n = 8 0 7 5 we get the desired sum of 2 0 1 6 . As the smallest k -value in our sum is 5 , we know that the next four integers after 8 0 7 5 will yield a sum of 2 0 1 6 as well.
Thus the desired solution is 8 0 7 5 + 8 0 7 6 + 8 0 7 7 + 8 0 7 8 + 8 0 7 9 = 4 0 3 8 5 .
Note that there are no n such that n ! ends in precisely 2 0 1 5 zeros, hence the title of this question.