Why not 6?
6 vertices are regularly spaced on the circumference of a circle. On each of the line connecting 2 of these vertices, a
non-negative integer
is placed. For any convex polygon with vertices on some of these 6 points, the sum of the integers written on their sides is less than or equal to 5.
Find the maximum possible value for the sum of all the written integers.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
[This is not a complete solution]
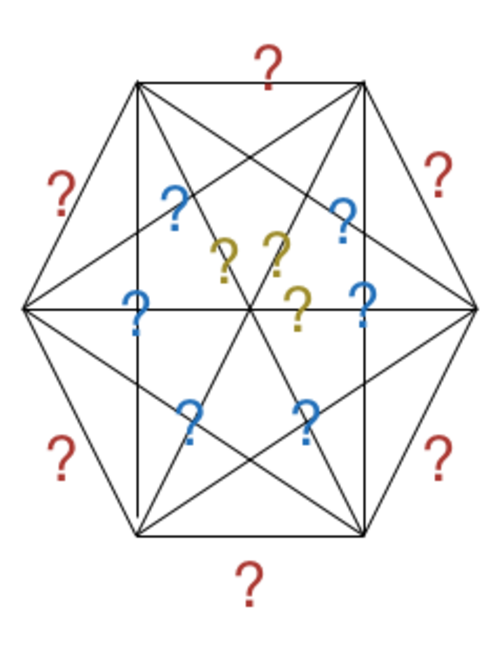
The above image demonstrates how to get a sum of 21. The red number correspond to distance 1 lines, the blue numbers correspond to distance 2 lines, and the yellow numbers correspond to distance 3 lines.
5 of the distance 1 lines are given a weight of 1, and 1 is given a weight of 0. For the rest, the weight of the line is the minimium of the sum of weights of the distance 1 lines going in either direction. As such, each line can be broken up into the distance 1 lines, and so it's clear that this configuration satisfies the conditions as stated.
It remains to show that this 21 is indeed maximal. If no one can do this after a week, ping me to update my solution.
Note: If you changed the problem to allow for real number to be placed instead, then the max is 22.5. The restriction to integer drops this below 22. The real number case and integer case have very similar solutions.