Why not displacement?
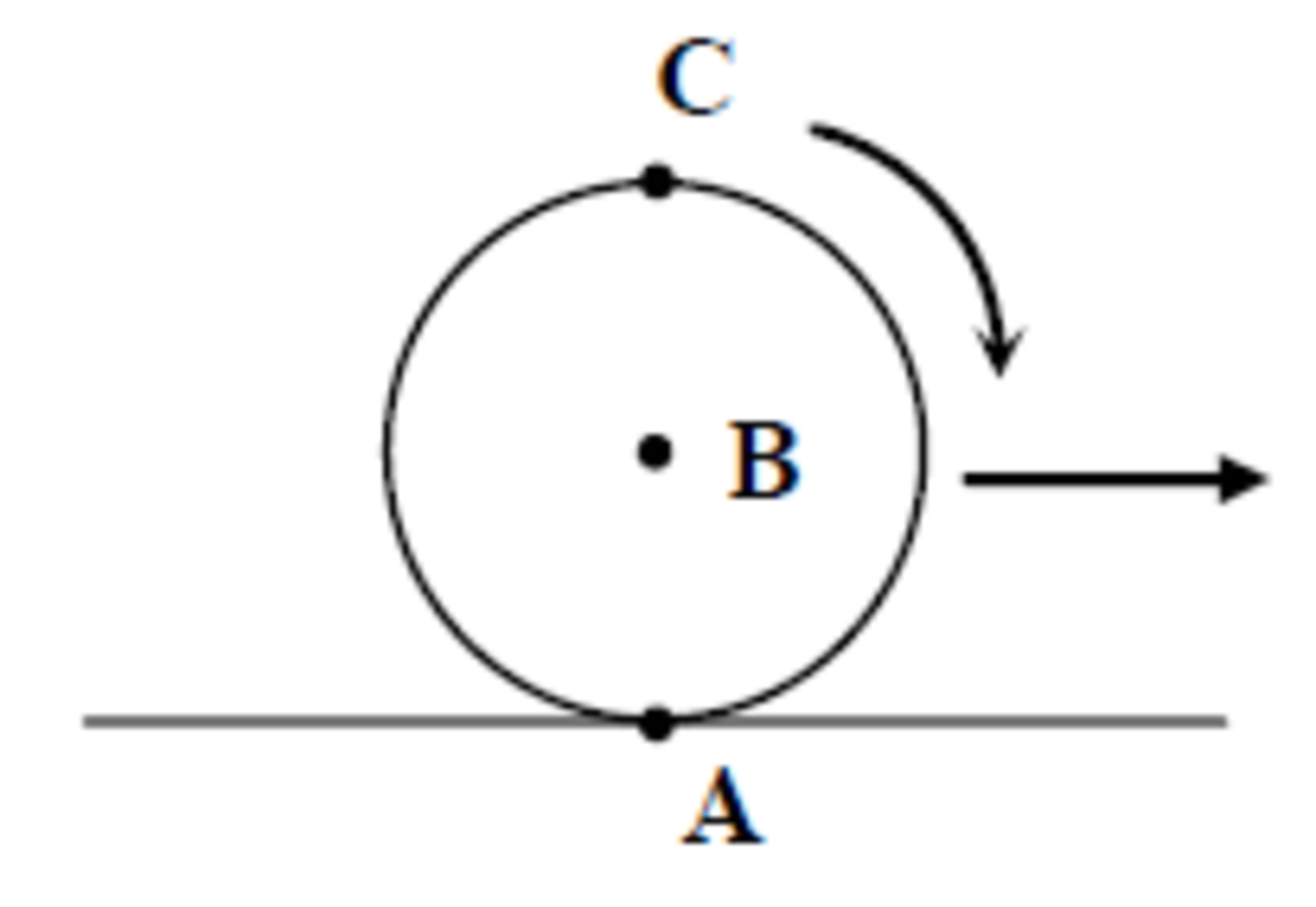
A cylinder of radius performs pure rolling on a horizontal surface. Find the distance travelled by the point which was initially in contact with the surface when one complete revolution is made by the the cylinder and the point touches the ground again.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The path of A is a cycloid, with equation x = R ( θ − sin θ ) y = R ( 1 − cos θ ) Thus we calculate that d θ d s = x ′ ( θ ) 2 + y ′ ( θ ) 2 = 2 R 2 ( 1 − cos θ ) = 4 R 2 sin 2 2 1 θ and hence d θ d s = 2 R ∣ ∣ sin 2 1 θ ∣ ∣ The distance A travels in a single revolution is 2 R ∫ 0 2 π sin 2 1 θ d θ = 8 R