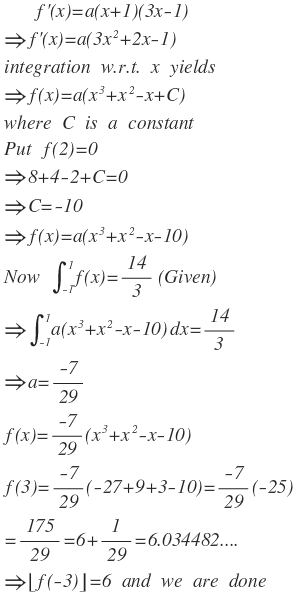Why so serious?
A cubic polynomial f ( x ) vanishes at x = 2 i.e f ( 2 ) = 0 and has a relative minimum/maximum at x = − 1 and x = 1 / 3 respectively. If
∫ − 1 1 f ( x ) d x = 3 1 4 ,
find ⌊ f ( − 3 ) ⌋ .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Suppose f ( x ) = a x 3 + b x 2 + c x + d . We then have that
f ( 2 ) = 8 a + 4 b + 2 c + d = 0 , (i).
Now since f ′ ( x ) = 3 a x 2 + 2 b x + c , we have that
f ′ ( − 1 ) = 3 a − 2 b + c = 0 , (ii), and
f ′ ( 3 1 ) = 3 a + 3 2 b + c = 0 ⟹ a + 2 b + 3 c = 0 , (iii).
Finally, ∫ − 1 1 f ( x ) d x = 4 a x 4 + 3 b x 3 + 2 c x 2 + d ∗ x ,
which when evaluated from x = − 1 to x = 1 results in the equation
3 2 b + 2 d = 3 1 4 ⟹ b + 3 d = 7 , (iv).
Solving equations (i) through (iv) simultaneously gives us that
a = − 2 9 7 , b = − 2 9 7 , c = 2 9 7 and d = 2 9 7 0 .
Thus f ( x ) = − 2 9 7 ( x 3 + x 2 − x − 1 0 ) , and so
⌊ f ( − 3 ) ⌋ = ⌊ − 2 9 7 ∗ ( − 2 5 ) ⌋ = ⌊ 6 . 0 3 4 4 . . . ⌋ = 6 .
Clearly the roots of quadratic function f'(x) are x=-1 and x=1/3 . So