Why the root , Dude ?
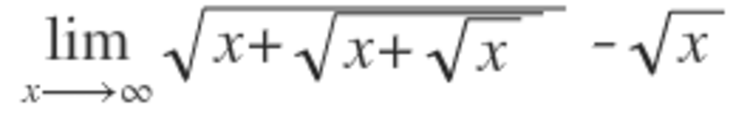 Here's a simple problem on Limits:
Here's a simple problem on Limits:
x → ∞ lim x + x + x − x
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
We can easily solve this problem by using rule#3 and rule#2 .
x → ∞ lim x + x + x − x if we see this kind of problems ,the first thing we need to do is to move the root and the best way to do that is by making it a^2-b^2[rule #3] so,
x → ∞ lim x + x + x + x ( x + x + x − x ) ( x + x + x + x )
x → ∞ lim x + x + x + x ( x + x + x ) 2 − ( x ) 2
so we get,
x → ∞ lim x + x + x + x x + x + x − x
now is the time to apply rule#2. Which is to divide both numerator and denominator by x^n [where x^n is the highest exponent of x containing in the fraction]
x → ∞ lim x x + x + x + x x x + x
x → ∞ lim x x + x x + x x + x x x x + x x
x → ∞ lim 2 + x x + x x 1 + x x
x → ∞ lim 2 + ( x ) 2 x + ( x ) 4 x 1 + x x
As x tends to infinity we get
2 + 0 + 0 1 + 0
hence we get the 1/2 which is also 0.5
Actually you cannot split x x + x = x x + x = x x + x x . The rest are also invalid too.
take x common, apply approximation .
just rationalize and divide both numerator and denominator by x ^ 1/2
x → ∞ lim x + x + x − x
= x → ∞ lim ( x + x + x + x ) ( x + x + x − x ) ( x + x + x + x )
= x → ∞ lim x + x + x + x x + x
= x → ∞ lim x x + x + x + x x x + x
= x → ∞ lim x + x + 1 + 1 x + 1
= x → ∞ lim x x + x + 1 + 1 x x + 1
= x → ∞ lim 1 + 1 + x 1 + x 1 1 + x 1
= 1 + 1 + 0 + 0 1 + 0 = 2 1 ~~~