Why Thomas, you're all wet!
If you've ever watched sailing, you will sometimes see a sailor hanging off the side of the boat, for example in this shot from the movie "The Thomas Crown Affair." Eventually, of course, the sailboat tips over so far that a person cannot keep it balanced. Consider an idealized model of a small sailboat where the boat is a point. We'll model the mast and sails as a 14 meter long uniform rod with total mass 400 kg. Our sailor will be modeled as a 100 kg point mass on the massless boom that extends 4 meters from the boat at a right angle to the sail. If θ is the angle between the mast and the horizontal axis, at what θ in degrees will the sailor be unable to keep the boat upright even if he is sitting at the end of the boom?
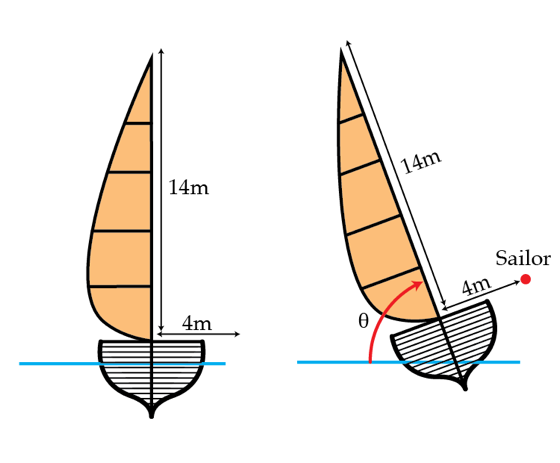
The answer is 81.87.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Clearly when the boat is upright ,the torque about the base point due to the weight of the rod (acting in anticlockwise direction in fig) must balance the torque due to the weight of the sailor(acting clockwise here).Now the weight of rod is concentrated about its center of mass and its perpendicular distance about the point of toppling i.e unbalance = 7cos(theta). Torque = |FxD|.Therefore torque due to the weight of rod = 2800cos(theta) Kg.m and torque due to weight of man =400 kg.m. Equating the two torques gives (theta)=cos^-1(1/7) =81.79 degrees.Hence once theta reaches this value,the sailor will be unable to keep the boat upright.
Here we have,
Mass of sailor, m1 =100 kg
Distance of sailor from point of rotation, l1 =4 m
Mass of mast, m2 =400 kg
Distance of mast from the point of rotation, l2 =7 m [since the mass is distributed along the whole rod so
The effective distance will be half the main length]
Now,
m1l1
sinθ =m2l2
cosθ [Initially the boat was erect but while sailing the boat, it
inclines at angle θ. Now if we consider the will balance
their moment horizontal direction, the effective length
becomes l2*cosθ. Similarly in the case of sailor ]
Or, θ= tan-1((m1l1)/(m2l2)) Putting the values, we get, θ=81.87
[solved]
Choose the pivot as the bottom end of the mast. The moments around this pivot are:
-
Counter-clockwise moment of weight of mast: τ c c w = m m a s t g d 1 ⊥ = m m a s t g ( 2 l 1 cos θ )
-
Clockwise moment of weight of sailor: τ c w = m s a i l o r g d 2 ⊥ = m s a i l o r g ( l 2 sin θ )
Principle of Moments: τ c c w = τ c w ⇒ m m a s t g ( 2 l 1 cos θ ) = m s a i l o r g ( l 2 sin θ ) ⇒ tan θ = m s a i l o r l 2 m m a s t l 1 ÷ 2 = 1 0 0 × 4 4 0 0 × 1 4 ÷ 2 = 7 ⇒ θ = arctan ( 7 ) = 8 1 . 9
as we are considering mast and sail as a uniform rod of length 14 m , we can assume its mass to at 7 m from the boat (center of mass) and thus torque along the boat will be T 1 = 7 ∗ 4 0 0 ∗ g ∗ cos θ .
And torque due to the sailor will be T 2 = 4 ∗ 1 0 0 ∗ g ∗ sin θ .
and as sailor is unable to keep the boat upright even if he is sitting at the end of the boom thus T 1 ≥ T 2 . . . . ( 1 )
by solving ( 1 ) we will get 7 ≥ tan θ
therefore θ = 8 1 . 8 7 degrees
At the critical angle where the boat is just about to tip over, the torque of the sailor and the torque of the mast are equal. We therefore have
τ M a s t = 2 1 m m a s t g L m a s t cos θ = m s a i l o r g l s a i l o r cos ( 9 0 − θ ) = τ s a i l o r .
This allows us to solve for tan θ = 7 which means θ = 8 1 . 8 7 degrees.
The sailboat tipping over is a consequence of angular velocity. The mast's weight and the sailor's weight apply torques to the boat.
Assume that we are at the limit of the sailor's capabilities-- that is, he is sitting at the end of the boom, yet his torque is completely balanced by the mast's torque. Then the angular acceleration will be zero and the boat will continue to tip despite the sailor's efforts.
T t o t = T m a s t + T s a i l o r = 0
T s a i l o r = − ( 1 0 0 ) g sin θ
Note the negative sign to denote the clockwise direction of the sailor's torque.
The mass of the mast and sails is considered to be distributed uniformly along a 14 meter rod. Because of this, for purposes of calculating torque, we can take the entire mass to be halfway along the rod, that is, at a distance of 7 meters from axis of rotation of the boat.
If you doubt this, consider integrating the torque from infinitesimal bits of weight.
T = ∫ 0 L r ( cos θ ) ( g M / L ) d r = ( L 2 / 2 ) ( cos θ ) ( g M / L ) = ( g M L / 2 ) cos θ
Then the torque from the mast and sails is:
T m a s t = g ⋅ 4 0 0 ⋅ 7 cos θ
Taking the torque balance from the beginning:
− T s a i l o r = T m a s t
4 0 0 g sin θ = 4 0 0 ⋅ 7 g cos θ
Solve for the angle:
θ = tan − 1 ( 7 ) = 8 1 . 8 7 ∘
These solutions depends on the simplifying assumption that the buoyancy of the sailboat, which depends on the cross section of the hull, is not a factor, i.e., the boat might as well be on dry land perched on its keel.
We can simplify the situation by taking out the boat and replacing the mast, boom and the sailor by two rods and a point mass respectively (as the question allows us to do/recommends).
In this case, then, the fulcrum/pivot will be the point at which the boat touches the water/ the meeting point of the mast and the boom.
Since the mast is a uniform rod (density is uniform throughout the rods structure), we can assume its center of mass to be at its center, i.e. its weight can be assumed to act at its center which is 14/2 = 7 m from the fulcrum. Thus, the moment of this force (the weight of the mast about the fulcrum along its length) is:
7 × 4 0 0 × 9 . 8 1 × c o s θ
(7 is the length in meters of the line along which the force acts, 4 0 0 × 9 . 8 1 is the weight of the mast(the force) and the c o s θ takes the component of the weight perpendicular to the line of action of the force, i.e. perpendicular to the mast itself)
The moment of the sailor about the boom is then:
4 × 1 0 0 × 9 . 8 1 × s i n θ
(4 m is the length of the line of action of the force about the pivot and s i n θ takes the component of the weight perpendicular to the line of action of this force)
The forces (weights) both act downwards so we need to take their components perpendicular to their respective lines of action (along the mast and boom).
When their moments are equal, any further decrease in θ will capsize the boat/ unbalance the moments so the maximum value of θ for which the boat will not capsize is given by
7 × 4 0 0 × 9 . 8 1 × c o s θ = 4 × 1 0 0 × 9 . 8 1 × s i n θ
⇒ 7 c o s θ = s i n θ
⇒ t a n θ = 7
Thus, solving this equation gives us
θ = 8 1 . 8 7 \circle