Width Mystery
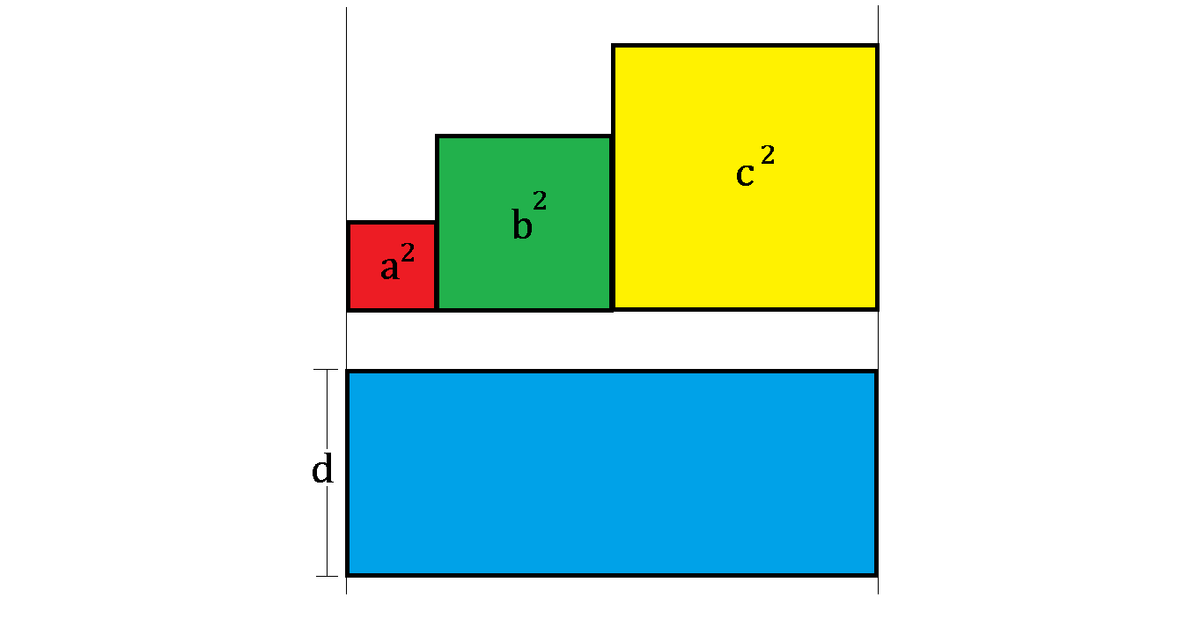
As shown above, the 3 colored squares have the side lengths of a < b < c while the blue rectangle has the length of a + b + c and the width of d .
If the blue rectangle's area is equal to the sum of 3 squares' areas combined, which of the following statements is correct?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
d ( a + b + c ) = a 2 + b 2 + c 2
Using the AM-GM inequality, equality cannot hold because a = b = c
d ( a + b + c ) > 2 a b + c 2
> 2 b c + a 2
> 2 c a + b 2
Adding these together:
3 d ( a + b + c ) > a 2 + b 2 + c 2 + 2 ( a b + b c + c a ) = ( a + b + c ) 2
3 d = d + d + d > a + b + c
We have that:
d ( a + b + c ) = a 2 + b 2 + c 2 ⇒ d = a + b + c a 2 + b 2 + c 2
By Titu's Lemma:
d = a + b + c a 2 + b 2 + c 2 = a + b + c a 2 + a + b + c b 2 + a + b + c c 2
≥ 3 ( a + b + c ) ( a + b + c ) 2
⇒ d ≥ 3 ( a + b + c ) ⇔ 3 d ≥ a + b + c
Equality holds when a = b = c = d , but we know that a < b < c . Hence the equality case must not hold.
Therefore, it is the case that:
d + d + d > a + b + c
a 2 + b 2 + c 2 = d ( a + b + c ) ⟹ ( a 2 + b 2 + c 2 ) ( 3 ) ≥ ( a + b + c ) 2 ⟹ 3 d ( a + b + c ) ≥ ( a + b + c ) 2 3 d = d + d + d ≥ a + b + c .
You have concluded that d + d + d ≥ a + b + c but that's not in one of the answer choices. There are > , < and = , but there is no ≥ . You must prove why equality case must not occur.
Relevant wiki: Power Mean Inequality (QAGH)
According to Power-Mean Inequality , the Quadratic Mean is more than or equal to the Arithmetic Mean of the data values:
3 a 2 + b 2 + c 2 ≥ 3 a + b + c
a 2 + b 2 + c 2 ≥ 3 ( a + b + c ) 2
a + b + c 3 ( a 2 + b 2 + c 2 ) ≥ a + b + c
From the question, a < b < c , so such equality will not hold for this case, and since the rectangle's area equals that of the three squares, then we can set up:
d ( a + b + c ) = a 2 + b 2 + c 2 . Thus, d = a + b + c a 2 + b 2 + c 2 .
As a result, 3 d = d + d + d > a + b + c .