Will angle chasing help?
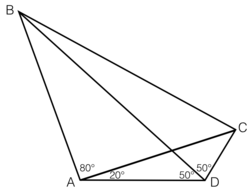 Quadrilateral
A
B
C
D
has angles
∠
B
D
A
=
∠
C
D
B
=
5
0
∘
,
∠
D
A
C
=
2
0
∘
,
and
∠
C
A
B
=
8
0
∘
.
Find
∠
B
C
A
(in degrees).
Quadrilateral
A
B
C
D
has angles
∠
B
D
A
=
∠
C
D
B
=
5
0
∘
,
∠
D
A
C
=
2
0
∘
,
and
∠
C
A
B
=
8
0
∘
.
Find
∠
B
C
A
(in degrees).
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
That is a very nice solution!
can you please do a full calculation of what you mean,it makes it easier for me to follow
just draw the angular bisector of angle ACD. Let it meet BD in Z. then quad BAZC is cyclic. Then after some simple angle chasing the problem is over.
Cool! Same way!!
Let us call the intersection point of A C and B D E and ∠ B C E = θ and ∠ E B C = α .Since D E is the internal bisector of angle D we have E C A E = D C A D . Applying sine-rule in △ A B E , △ B E C 2 A E = sin 8 0 ∘ B E sin α E C = sin θ B E ⟹ 2 D C A D sin α = sin 8 0 ∘ sin θ . Leave that aside for a second and apply sine-rule in △ A B D , △ B D C ,we get, 2 A D = sin 1 0 0 ∘ B D sin α D C = sin ( 6 0 + θ ) B D ⟹ 2 D C A D sin α = sin 1 0 0 ∘ sin ( 6 0 + θ ) ⟹ sin 1 0 0 ∘ sin ( 6 0 + θ ) = sin 8 0 ∘ sin θ ⟹ sin ( 6 0 + θ ) = sin θ Expanding the left hand side and evaluating we obtain tan θ = 3 , hence θ = 6 0 ∘ .And done!
Moderator note:
Nice solution.
When applying a formula, it is best to leave it in the recognizable form, so that the reader can quickly follow what you are saying. IE Use sin 3 0 ∘ A E instead of 2 A E , and the reader will immediately say "Ah yes, that is sin α a .
Sorry for the late response,sir and thank you for the advice,i will definitely be careful about this when I write my next solution :)
With out loss of generality, let AB=1, and angle BCA=X.
∠
A
C
D
=
1
8
0
−
2
0
−
5
0
−
5
0
=
6
0
Applying Sin Law to triangles ABC, ABD, CBD, we get
B
C
1
=
S
i
n
8
0
S
i
n
X
,
1
B
D
=
S
i
n
5
0
S
i
n
1
0
0
,
B
D
B
C
=
S
i
n
(
6
0
+
X
)
S
i
n
5
0
,
Equating the product of the left sides of the three equations with the right sides, we get,
1
=
S
i
n
8
0
S
i
n
1
0
0
∗
S
i
n
(
6
0
+
X
)
S
i
n
X
,
B
u
t
S
i
n
(
6
0
+
X
)
S
i
n
X
=
S
i
n
6
0
C
o
t
X
+
C
o
s
6
0
1
⟹
S
i
n
6
0
C
o
t
X
+
C
o
s
6
0
=
S
i
n
8
0
S
i
n
1
0
0
.
C
a
l
c
u
l
a
t
i
n
g
,
X
=
6
0
Most probably angle DBC will be shorter than 30° hence either DBC could be 10 or 20 (assumption) by substituting 10 you get answer 60 while you have 3 tries and you have two cases hence you will be able to get answer (I know its hilarious)
We have AB is external bisector of CAD and DB is internal bisector of CDA. Then, we have CB is external bisector of ACD. So ,we have ACB=(180-60):2=60