Will Angle Chasing Work?
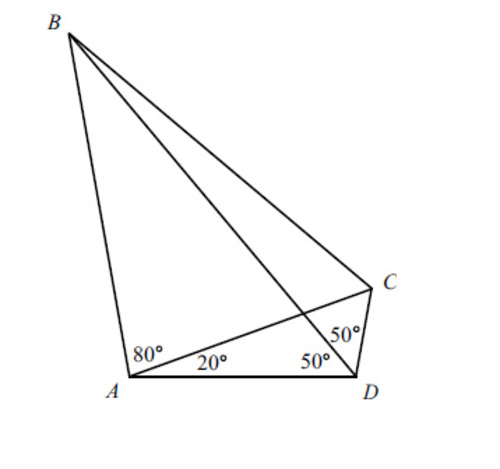 In the figure
∠
B
D
A
=
∠
C
D
B
=
5
0
∘
,
∠
D
A
C
=
2
0
∘
,
∠
C
A
B
=
8
0
∘
In the figure
∠
B
D
A
=
∠
C
D
B
=
5
0
∘
,
∠
D
A
C
=
2
0
∘
,
∠
C
A
B
=
8
0
∘
If ∠ B C A = x ∘ , ∠ D B C = y ∘
Then find the sum of the digits of the number x y .
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Great job! I actually used sine rule. But your solution must be the best way to do it.
B is the intersection of the external angle bisector of angle CAD and the angle bisector of angle ADC. Thus B is the centre of the excircle opposite D. Thus BC is the external angle bisector of angle ACD, and angle BCA is 60°. Thus
x = 6 0 , y = 1 0 , x y = 6 0 4 6 6 1 7 6 0 0 0 0 0 0 0 0 0 0 which has sum of digits 36.
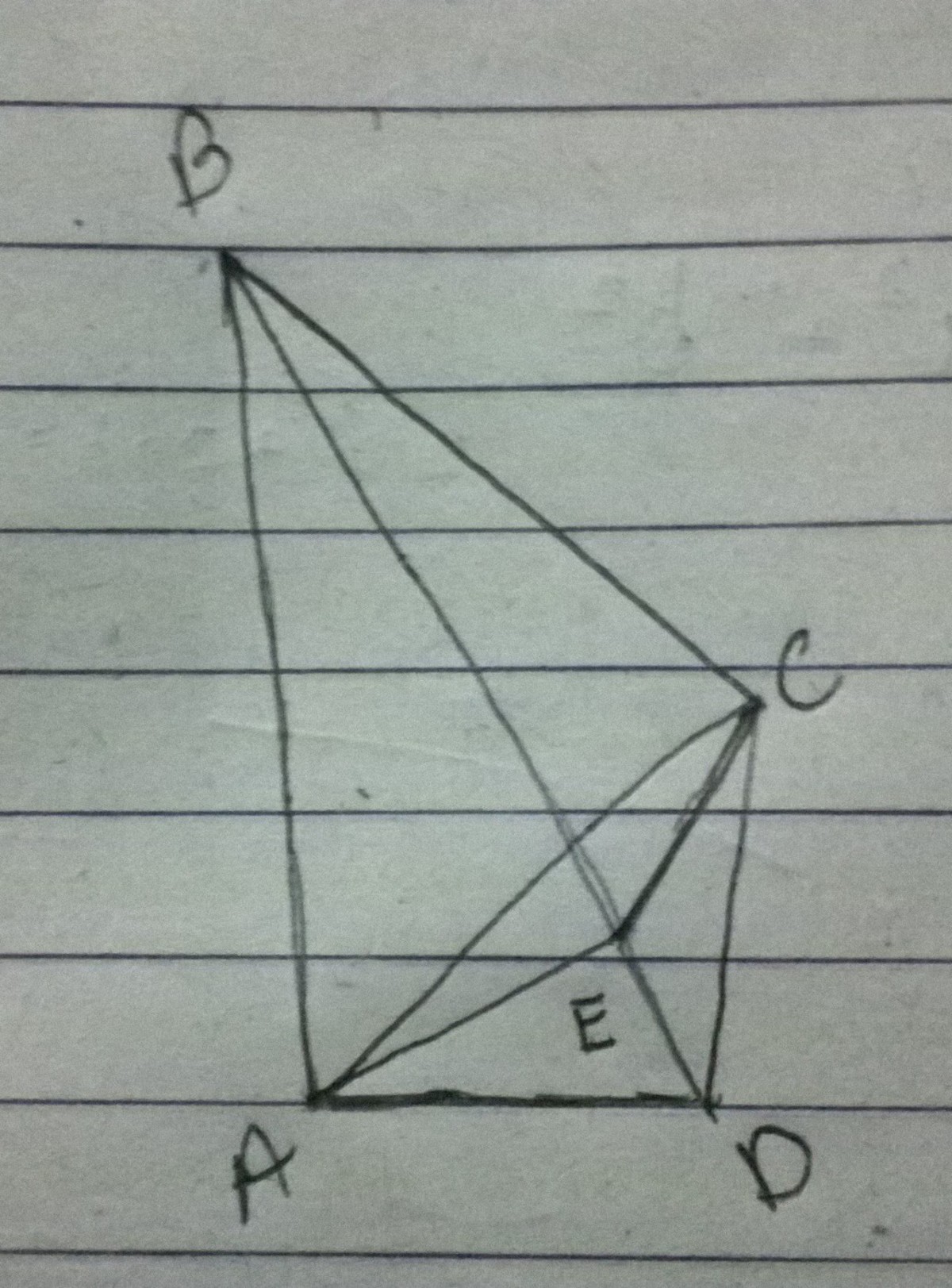 Draw angle bisector of
∠
B
C
D
meeting BD at E
Draw angle bisector of
∠
B
C
D
meeting BD at E
Now.
Since ∠ A B E = ∠ A C E = 3 0
Therefore ABCE is cylic
Also since angle bisectors of ∠ D and ∠ A C D meet at E.
Therefore E is the incentre of △ A D C
So,
∠ F A E = 1 0
This gives,
x = ( 1 8 0 − 9 0 ) − 3 0 = 6 0
So
y = 1 0
Now,
x y = 6 0 1 0 = 6 1 0 × 1 0 1 0 = 6 0 4 6 6 1 7 6 × 1 0 1 0
Therefore ,
Sum of digits = 3 6
AXD = 180 - (DAC + BBA) = 110 (Angles in a triangle make 180)
BXC = AXD = 110 (Opposite Angles)
AXB = 180-BXC = 70 (Angles in a straight line)
CXD = AXB = 70 (Opposite Angles)
ABD = 180 - (CAB + AXB) = 30 (Angles in a triangle make 180)
I can see 2 methods for getting reming 2 angles :
Construction or Sin Rule (Both require a random length for starting point which is fine as it is only angles we care about)
I went with construction and got BCA = 60 & DBC = 10
60^10 = 6^10 * 10^10
6^10 * 10^10 = 60466176 * 10000000000
==> 6+0+4+6+6+1+7+6 +(10*0)= 36
We have ∠ A B D = 3 0 ∘ and ∠ A C D = 6 0 ∘ . Let the angle bisector of ∠ A C D intersect B C at P . Then, ∠ A C P = ∠ A B P = 3 0 ∘ , so A B C P is cyclic. Since C P and B D are both angle bisectors of △ A C D , they intersect at the incenter of △ A C D , which is P . Thus, ∠ C A P = ∠ C B D = 1 0 ∘ and ∠ B C A = 6 0 ∘ . Finally, x y = 6 0 1 0 , which has digit sum 3 6 .