Will the goldfish hit the waves?
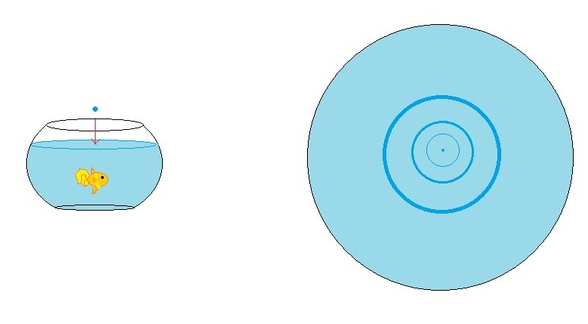
A water droplet falls into the fish bowl, rippling the water surface from the center. As shown above, the circular waves will spread out in continuous enlarging circles at a constant rate, at which its outermost wave will reach the full circular edge of water surface within some period of time, . At some point during that time lapse , the goldfish will emerge, gulping for air, randomly over somewhere on the water surface.
What is the probability that the goldfish will be within the biggest wave circle and so hit the waves? If the answer is in a form of for some co-prime , enter as the answer.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let r be the radius of the outermost wave radius, R be the radius of the whole water surface, t be the time under T that is the total time needed for outermost wave to reach the full circle, as in the question.
The probability of the goldfish hitting the waves at any time t is P ( t ) = π R 2 π r 2 = R 2 r 2 .
To find the probability for the goldfish hitting the waves over the time lapse T , we can calculate as:
T 1 ∫ 0 T P ( t ) d t
Now since the waves spread in circles at a constant rate, that means at d t d r = k for some constant k . In other words, r ( t ) = k t for some linear progression since we know r = 0 at t = 0 . Also, we know that r ( t = T ) = R = k T because the whole radius is reached at t = T . We can conclude k = T R . Hence, r = T R t , or R r = T t .
To visualize it, we can set up the stacks of radii as time passes to T as similar triangles, as shown below:
Thus, the desired probability equals: T 1 ∫ 0 T P ( t ) d t = T 1 ∫ 0 T R 2 r 2 d t
Substituting R r = T t , we will get:
T 1 ∫ 0 T R 2 r 2 d t = T 1 ∫ 0 T T 2 t 2 d t = T 3 1 ∫ 0 T t 2 d t = T 3 1 [ 3 t 3 ∣ ∣ ∣ ∣ 0 T ] = T 3 1 [ 3 T 3 − 0 ] = 3 1
Thus, the probability equals 3 1 . Alternatively, we can also visualize the circle stacks of "time" at each instant and integrate them all, as followed: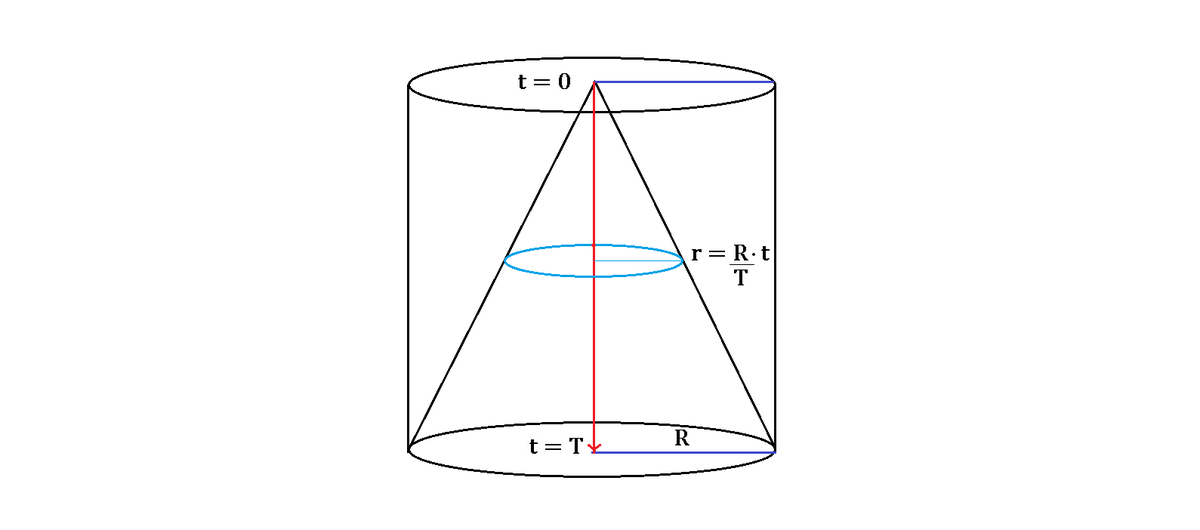
Clearly, the integrated areas will become volumes of a cone and a cylinder of the same radius R and "height" T , and by the conic volume formula, the ratio is simply 3 1 .