Will you count?
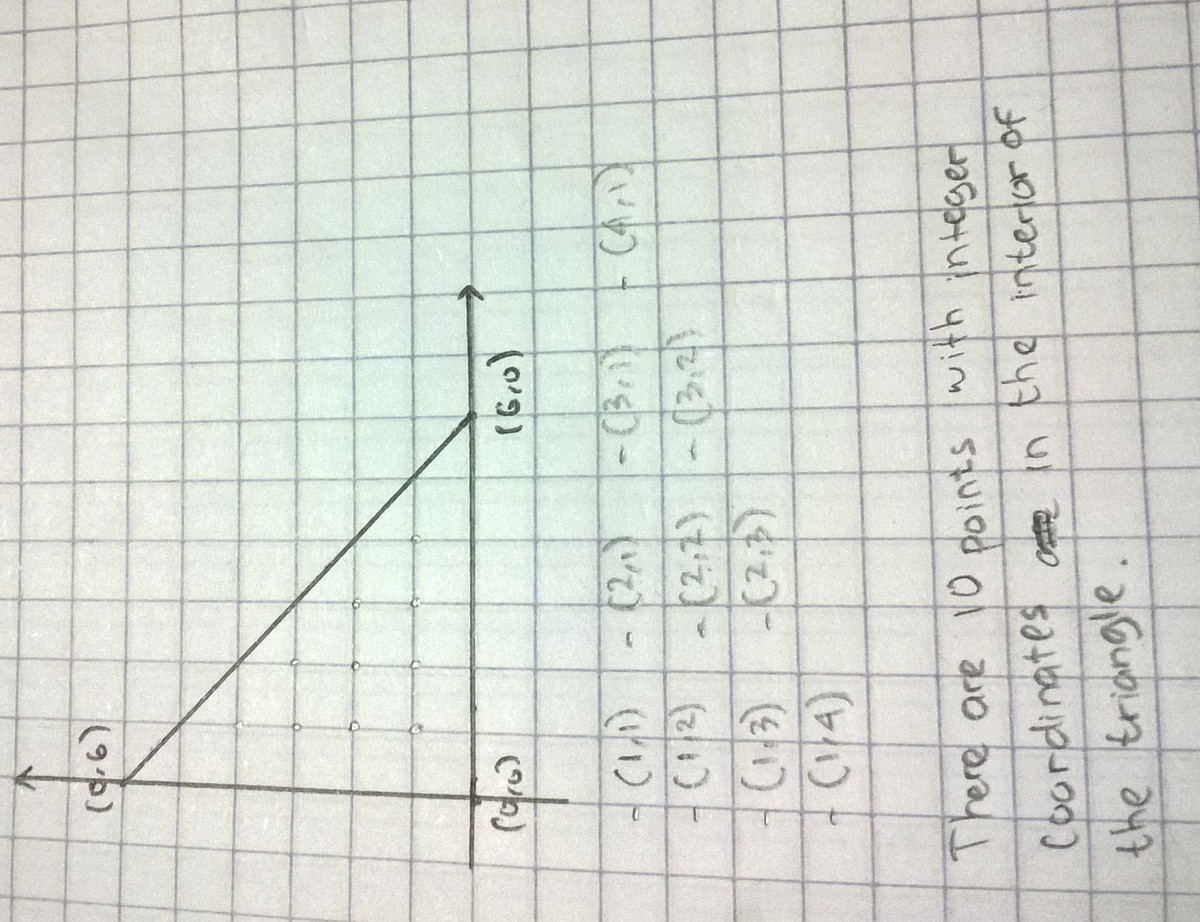
A triangle is formed by the points ( 6 , 0 ) , ( 0 , 0 ) , ( 0 , 6 ) . How many points with integer coordinates are in the interior of the triangle?
Bonus Generalize this.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
In General
2 (no. of integral point)=(n-1)(n-2)
here, n=6
no. of integral point=10
Triangle's area is 1 8 due to is a rectangle triangle of cathets 6
Area = I + 2 B − 1
I = number of points in the interior of the polygon
B = number of points on the boundary of the polygon
Counting B
On the vertical are (0,0), (0,1), (0,2), (0,3), (0,4), (0,5), (0,6)
On the horizontal are (0,0), (1,0), (2,0), (3,0), (4,0), (5,0), (6,0)
On the diagonal are (0,6), (1,5), (2,4), (3,3), (2,4), (1,5), (0,6),
B = 1 8
Now, substituing
1 8 = I + 2 1 8 − 1 ∴ I = 1 0
Same! And I guarantee this solution for everybody.
In the the interior of any triangle with coordinates as (0,0) , (n,0) and (0,n). The number of integer coordinates would be
(1,1) (1,2) ........... (1, n-2)
(2,1) ...............(2,n-3)
And so on upto
(n-2,1)
Thus the total no. of integer coordinates would be 1 + 2 + 3.........n-2. Which is equal to
(n-2)(n-1)/2
Putting in n as 6 here we get the desired answer which is 10.