Will you roll with me?
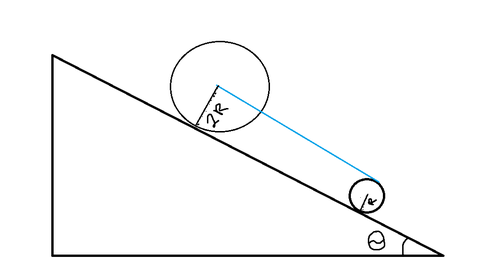 Two rigid uniform cylinders each of mass
5
0
k
g
are placed on a rigid and rough inclined plane at an angle of
3
0
∘
above the horizontal. A massless string connects the axle of the larger cylinder to the rim of the smaller one. If both of the cylinders roll without slipping, what is the acceleration of the smaller cylinder?
Two rigid uniform cylinders each of mass
5
0
k
g
are placed on a rigid and rough inclined plane at an angle of
3
0
∘
above the horizontal. A massless string connects the axle of the larger cylinder to the rim of the smaller one. If both of the cylinders roll without slipping, what is the acceleration of the smaller cylinder?
Details and Assumptions
g is 9 . 8 1 s 2 m
The answer is 1.962.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
How did you Know that friction is Limiting ? In Actual You Should have To write friction as unknown ' f ' instead of writing it as Kinetic ! Because friction is Rolling which is not equal to kinetic friction. In-fact f s t a t i c , ( L i m i t i n g ) > f k i n e t i c > f R o l l i n g . So Please Kindly Recheck this !
I did in the same way!
Log in to reply
@satvik pandey Could you explain why angular acceleration is the same for both of them?
Smaller cylinder can be taken as winding upwards. Writing torque equation about centre of mass for small cylinder we get - Let the tension in the string be T Therefore , RT + Rmgsin30 = mr^2/2 * (a/r) ........ (1) Writing torque equation about inclined on bigger sphere - 2RT = 3mr^2/2 * (a/2R) 2T = 3ma putting in (1) a = 1.96m/s^2
This question is incomplete as it has to be mentioned that the friction is limiting.
If mentioned, it is Level 3 problem.
Log in to reply
Nope. I Took The Frictions At Two Contact Points As f1 and f2 and solved the problem correctly
L e t s s a y a c c e l e r a t i o n o f b i g g e r c y l i n d e r i s a 1 a n d a c c e l e r a t i o n o f s m a l l e r c y l i n d e r i s a 2 P U R E R O L L I N G : a 1 = ( 2 R ) α . . . . . ( 1 ) a 2 = ( R ) α . . . . . . ( 2 ) a 1 = 2 a 2 . . . . ( 3 ) f o r c − 1 : m g s i n θ − T − η m g c o s θ = m a 1 f o r c − 2 : T + m g s i n θ − η m g c o s θ = m a 2 e l i m i n a t i n g T : 2 m g s i n θ − 2 η m g c o s θ = 3 m a 2 . . . . . . ( 4 ) T o r q u e a b o u t C . O . M o f b i g g e r c y l i n d e r : η m g c o s θ ( 2 R ) = 2 m ( 2 R ) 2 . α η m g c o s θ = m a 2 . . . . . . . ( 5 ) u s i n g ( 4 ) a n d ( 5 ) : 2 m g s i n θ = 5 m a 2 a 2 = 1 . 9 6 2 s 2 m