Win that stuffed toy
At the local games arcade, you have to toss a circular disc of diameter 5 onto a grid of 3 × 3 squares, each of which has side length 10. You win a stuffed toy if your disc does not touch any of the grid lines. You are playing the kiddie version, where walls are set up on the sides to ensure that the disc will be contained entirely within the grid. Assume that the position of your thrown disc is distributed uniformly, the probability that it lands entirely in a grid square can be expressed as b a where a and b are coprime positive integers. What is the value of a + b ?
Details and assumptions
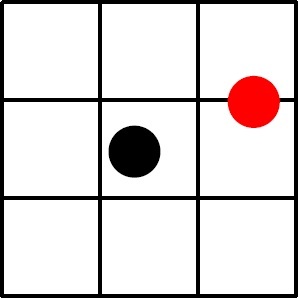
In the figure below, the black disc is entirely in a grid square, but the red disc is not.
The answer is 34.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
View the diagram here
Hence, the probability is 2 5 × 2 5 9 × ( 5 × 5 ) = 2 5 9
No permission to view...
Log in to reply
Sorrry! Can you please try again? I made it public now
Nice graph, clear and explicit.
Sample area = ( 3 0 − 2 ∗ 2 . 5 ) ∗ ( 3 0 − 2 ∗ 2 . 5 ) = 2 5 ∗ 2 5
Event area = 9 ∗ ( 1 0 − 2 ∗ 2 . 5 ) ∗ ( 1 0 − 2 ∗ 2 . 5 ) = 9 ∗ 5 ∗ 5
So probability = 2 5 9
Answer: 9 + 2 5 = 3 4
For each 1 0 × 1 0 square, the center of the disk must be in a 5 × 5 region. The center of the disk can only be in a 2 5 × 2 5 region, so the answer is 2 5 9 .
Let the centre of the disk be O .
Within one of the squares, the area of the O can move to win the stuffed toy is ( 1 0 − 2 . 5 − 2 . 5 ) ( 1 0 − 2 . 5 − 2 . 5 ) = 2 5 . Then among all the squares, the area of the O can move is 9 × 2 5 = 2 2 5 .
The total area of O can move is ( 3 0 − 2 . 5 − 2 . 5 ) ( 3 0 − 2 . 5 − 2 . 5 ) = 6 2 5 .
Hence, the answer is 6 2 5 2 2 5 = 2 5 9 . a + b = 3 4 .
We will consider the center of the circle.. for the circle to lie within the 3 × 3 grids surrounded by walls , its center always has to be atleast 2.5cm away from each of the boundry walls..giving us total usable area as 3 0 − 2 × 2 . 5 ) 2 =625 ... and for the circle to lie within an 1 0 × 1 0 grid its center has to be atleast 2.5cm away from each of the 1 0 × 1 0 grid lines..giving us total required area as ( 1 0 − 2 × 2 . 5 ) 2 = 2 5 now like this there are 9 grids..total probabality becomes ( 2 5 × 9 ) \6 2 5 = ( 9 \2 5 )
We can find the successful area and the total area for the center of the disk, which will give us the answer.
The successful area for the center of the disk consists of a region inside each of the 9 little squares. These regions are squares with side-length 1 0 − 2 ⋅ 2 . 5 = 5 , and hence have total area 9 ⋅ 2 5 = 2 2 5 .
The total area for the center of the disk consists of a region inside the big square, since the entire disk must land inside the square. This side-length is, similarly, 3 0 − 2 ⋅ 2 . 5 = 2 5 , and so the total area is 6 2 5 .
The probability is 6 2 5 2 2 5 = 2 5 9 , and the answer is 9 + 2 5 = 3 4 .