Winching a Rod

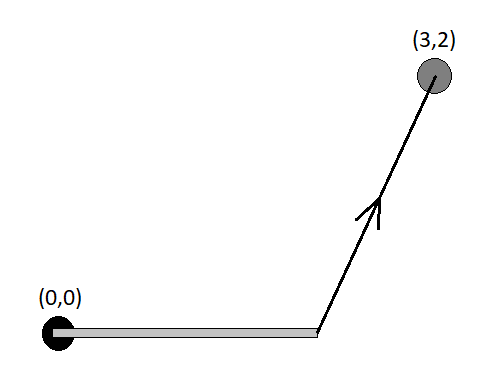
A rod of mass $M$ and length $L$ has one end hinged at the origin in the $xy$ plane. Its other end is connected to a cable, which is connected to a winch at $(x,y) = (W_x,W_y)$ . The winch keeps a constant tension $T$ on the cable, and the length of extended cable varies as the rod moves.

At time $t = 0$ , the rod is horizontal, stationary, and pointed in the $+x$ direction. At what time is the rod colinear with the origin and the winch? If the answer is $t_f$ , give your result as $\lfloor 1000 \, t_f \, \rfloor$ .

Details and Assumptions:
- $\lfloor \, \cdot \, \rfloor$ denotes the floor function
- There is no gravity
- $M = 10 \, \text{kg}$
- $L = 2 \, \text{m}$
- $T = 5 \, \text{N}$
- $(W_x , W_y) = (3 \, \text{m}, 2 \, \text{m})$