Winding around a pole a with a conducting spring.
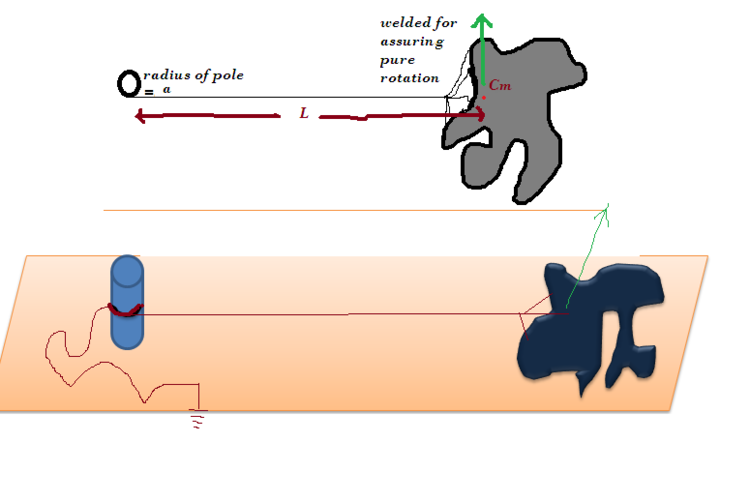 A laminar body of mass m made of insulating material carrying some amount of charge is attached (welded) to one end of a extremely strong and very stretchable spring of almost zero equilibrium length. The other end of which is fixed wound to fixed non conducting pole and then grounded. The spring constant initially is K. Initial conditions are set up so the mass moves around a cylindrical pole of radius a on a frictionless horizontal table. L is the initial distance from the centre of mass to the pole.We start by giving a velocity to the lamina as shown. The spring winds around the pole and the lamina eventually hits the pole . What amount of charge in
is lost from the lamina at half of the total time before collision if the electrostatic potential at the centre of the pole at that time is V.The spring is made of conducting material of resistance R
A laminar body of mass m made of insulating material carrying some amount of charge is attached (welded) to one end of a extremely strong and very stretchable spring of almost zero equilibrium length. The other end of which is fixed wound to fixed non conducting pole and then grounded. The spring constant initially is K. Initial conditions are set up so the mass moves around a cylindrical pole of radius a on a frictionless horizontal table. L is the initial distance from the centre of mass to the pole.We start by giving a velocity to the lamina as shown. The spring winds around the pole and the lamina eventually hits the pole . What amount of charge in
is lost from the lamina at half of the total time before collision if the electrostatic potential at the centre of the pole at that time is V.The spring is made of conducting material of resistance R
Neglect any sort of electrostatic interactions or energy/
assume find (the required charge in micro C) + 10.11 as the final answer
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A very important thing to think about while approaching is that the angular momentum is not conserved in this problem because the force is not a central force. Let θ ( t ) be the angle which the spring moves.Let x ( t ) be the length of the unwrapped part of the spring.let v ( t ) be the mass. And let k ( t ) be the spring constant as a function of time. note that the spring constant is not constant as it depends on the length.
I'll explain this
The spring constant of the unwrapped part of the spring is inversely proportional to its equilibrium length .(for example if you cut the spring in half the resulting springs will have twice the original spring constant) All the equilibrium lengths are infinitesimally small as compared to the L but the inverse relation between k and l still holds.
If you want some more reasoning then think of the equilibrium length as a measure of the total number of spring atoms that remain in the unwrapped part.
Using the approximation a ≪ L we may say that the mass undergoes approximate circular motion.This approximation will break down when x becomes close to a but that time is extremely negligible of the total time. The instantaneous centre of the circle is the point where the centre touches the pole.Alone the radial direction
x m v 2 = k x
ω = d t d θ = x v = m k
note that the change in angle of contact point on the pole equals the change in angle of the mass around the pole which is θ
Consider a very small interval during which the unwrapped part of the spring stretches a small amount and moves through an angle d θ
then a length a d θ becomes unwrapped on the pole so the fractional decrease in the equilibrium length of the unwrapped part is to the first order in d θ
and is equal to x a d θ
Hence the new spring constant is k n e w = ( 1 + x a d θ ) k o l d ≈ k o l d ( 1 − x a d θ )
therefore d k = x k a d θ
dividing by dt
d t d k = x k a ω
The final equation we need is the one for energy conservation. At a given instant consider the sum of the kinetic energies of the mass, and potential energy of the unwrapped par of the spring.At a time dt later a tiny bit of this energy will be stored in the newly wrapped light piece.Letting primes denote quantities at this latter time, conservation of energy gives
2 k x 2 + 2 m v 2 = 2 k ′ x ′ 2 + 2 m v ′ 2 + 2 k x 2 x a d θ
The last term is to the lowest order in d θ is the energy stored in the newly wrapped part. because a d θ is its length
writing v in terms of x
we get
k x 2 = k ′ x ′ 2 + 2 k x a d θ
in other words
d ( k x 2 ) = − 2 k x a d θ again dividing by dt
d t d ( k x 2 ) = − 2 k x a ω = d t d k x 2 + 2 k x d t d x = ( x k a ω ) x 2 + 2 k x d t d x
therefore d t d x = − 4 3 a ω .......1
we must now solve the two coupled differential equations.
x d t d x = − 4 3 k d t d k
∫ L x x d x = − ∫ K k 4 3 k d k
k = x 3 4 K L 3 4 ....2
from 2 and 1, therefore putting the value of \omega we get
x 2 / 3 d t d x = − 4 m 2 1 3 a K 2 1 L 3 2
on integrating we get and putting initial conditions x=L t=0
x 3 5 = L 3 5 − ( 4 m 2 1 5 a K 2 1 L 3 2 ) t
so finally we get
x ( t ) = L ( 1 − T t ) 5 3 ...........3
T = 5 a 4 L K m is the total time before the mass collides
But its not over yet
Now comes the part of of electricity and magnetism
For a lamina rotating about a pole let us say a point because of approximations
Let us consider an elemental arc of charge dq at a radius r_{i} from the pole
The current due to this charge is d i = 2 π ω d q in circular motion
B due to a ring at its centre is given by B = 2 π r μ I = 2 ( 2 π ) μ ω ∑ r i d q = μ ε 0 V ω
As number of loops around the pole is increasing with time the effective area of the loops is
A ( t ) = 2 π a ( L − x ) π a 2
ϕ = ∮ B . d A = B A ( t ) = μ ε 0 V ω 2 π a ( L − x ) π a 2
d t d ϕ = R d t d i
Solving these equations and putting necessary information we get
△ Q = 2 R m K μ ε 0 V a L ( 1 − T t ) 5 2 ( 1 − ( 1 − T t ) 5 3 )
We get the final answer as 23