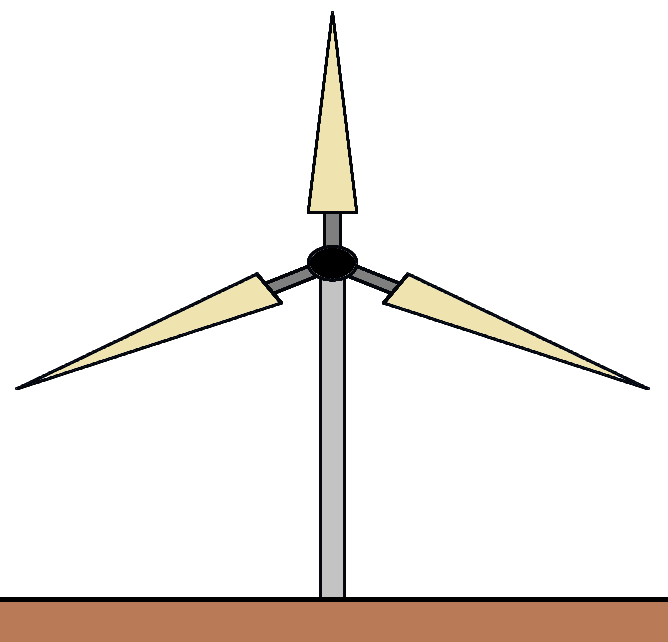
Wind(less) Turbine Support Reaction

Classical Mechanics Level 4

A wind turbine has three identical blades which are spaced apart by $120$ degrees. Let the total weight of the resting wind turbine be $W$ , and let $F$ be the magnitude of the total reaction force at the anchor point of the tower.

Let $F_{max}$ be the maximum value of $F$ over time. What is the relationship between $F_{max}$ and $W$ ?

Details and Assumptions:
- The blades are spinning with constant nonzero angular speed
- Neglect interactions between the blades and the air. Assume that some Brillianters are running this experiment using a miniature turbine contained within a vacuum chamber. They are trying to resolve disagreements about how to calculate these reaction forces, and they want to minimize confounding factors.

As a follow-up to this problem, try this one

\large{F_{max} = W}

\large{F_{max} < W}

\large{F_{max} > W}

1 solution

Tapas Mazumdar
May 26, 2018

$F_{max}$ would be equal to the magnitude of the resultant force of the vector addition of the two forces : Centripetal force on the blades and the weight of the blades. Regardless of whatever angular speeds the blades move with, due to the angle being $120^{\circ}$ between them, the resultant of the centripetal forces cancel out in the horizontal direction (i.e. in the axis parallel to the plane of the blades) and in the vertical direction only the total weight of the blades contribute to the net normal reaction force. Thus $F_{max} =W$ is the correct choice.

Wind(less) Turbine Support Reaction

1 solution

0 pending reports