Winner moves

Probability Level 3

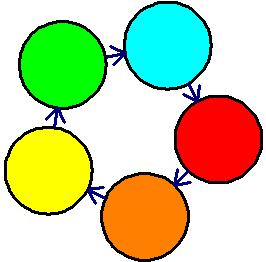
You are one of ten friends who are going to play a few rounds of a simple two-player game of chance. Each player has a 50 % 50\% chance of winning the game each round.

In the beginning, two people go to each colored circle. Each round the people at a circle play the game and determine the winner. A round ends when the winner follows the arrow to the next circle. The loser stays where they are.

After 10 rounds, what is the probability you are on the circle you started on?

The answer can be written as a fraction, a b \frac{a}{b} . If this fraction is in lowest terms, enter the value of a + b a+b .


The answer is 639.

Jeremy Galvagni by Jeremy Galvagni , 48, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Jeremy Galvagni
Jul 11, 2018

Each round is a binomial trial with n = 10 n=10 and p = 1 2 p=\frac{1}{2} There are three distinct ways to end in the circle you start in: win zero times, win five times or win 10 times.

P ( 0 ) = P ( 10 ) = 1 2 10 = 1 1024 P(0)=P(10)=\frac{1}{2^{10}}=\frac{1}{1024}

P ( 5 ) = ( 10 5 ) 2 10 = 252 1024 P(5)=\frac{\binom{10}{5}}{2^{10}}=\frac{252}{1024}

The sum is 254 1024 = 127 512 \frac{254}{1024}=\frac{127}{512} so a + b = 127 + 512 = 639 a+b=127+512=\boxed{639}

6 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...