This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
Did it in the same way
Ahhhh, thank you
When you multiply two numbers with powers, you add their exponents. So this comes out to be 2/2 which is 81^1
That's right!
just -1 over 2 + 3 over 2 which is 1 so the answer is just 81^1 which is 81
Moderator note:
Good. It is easier to apply the rules of exponents to the powers first, rather than simplify each individual term.
8 1 − 2 1 × 8 1 2 3 = 8 1 − 2 1 + 2 3 = 8 1 2 2 = 8 1 1 = 8 1
just -1 over 2 + 3 over 2 which is 1 so the answer is just 81^1 which is 81
3/2 - 1/2 = 2/2 = 1; 81^(1) = 81
81^-1/2 x 81^3/2
1/81^1/2 x (81^1/2)^3
1/9 x 9^3
9^2
81
81^-1/2 x 81^3/2
Take 81 common
81^3/2-1/2
81^2/2
81^1 = 81
There is a rule of multiplication , that is if same bases are multiplying , then their powers will be added, so if we add -1/2+3/2 it will be equals to 1 and any no. Whose power is 1 will remain same .
8 1 − 1 / 2 × 8 1 3 / 2 = 8 1 3 / 2 − 1 / 2 = 8 1
=(81^-1/2)*(81^3/2) =81^((-1/2)+(3/2)) =81
1/2 + 3/2 = 2/2 = 1 so 81^1 = 81
First(81^-1/2 )(81^3/2)=81^(-1/2+3/2)=81^2/2= 81^1=81
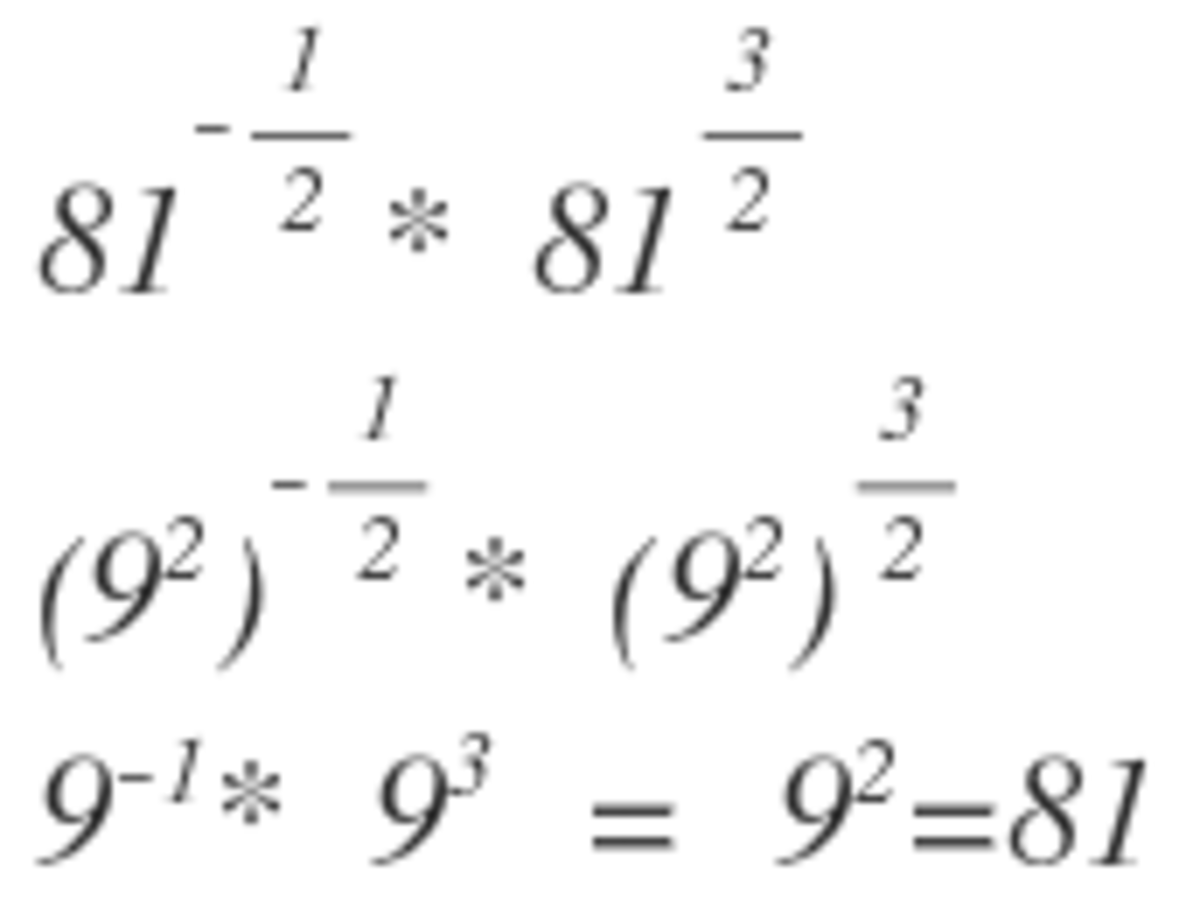
We have the expression 8 1 − 1 / 2 × 8 1 3 / 2 . Using the rules of exponents , we have the above expression as \[\begin{array}{} & = 81^{-1/2 +3/2} \\ & = 81^1 \\ & = 81. \square \end{array}\]