Winter Holiday Homework---- Radical Expression #2
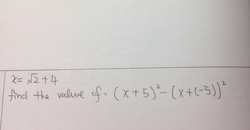 Find the value of. Note your answer should be in one decimal place, e.g: 123.4
Find the value of. Note your answer should be in one decimal place, e.g: 123.4
The answer is 108.3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
We are given that x = 2 + 4
Substituting x into the equation given gives us: ( 2 + 9 ) 2 − ( 2 − 1 ) 2 Which, by expanding the brackets, gives us: ( 8 3 + 1 8 2 ) − ( 3 − 2 2 ) Simplifying by collecting alike terms: 8 0 + 2 0 2 Which can be either put into a calculator, or worked out manually using the approximation: 2 ≈ 1 . 4 1 4
8 0 + 2 0 × 1 . 4 1 4
= 8 0 + 2 8 . 2 8
= 1 0 8 . 2 8
= 1 0 8 . 3 correct to 1 decimal place, as requested.
The given expression is in the form (a + b)^2 - (a - b)^2. Therefore the resulting answer will be in the form 4ab. Therefore the value of it is 4(sqrt(2) + 4)(5),which results in 108.3.(approx)