Winter solstice

We first consider the case without the inclination of the earth, so that all points on the earth move through the rotation of the earth on circular paths parallel to the xy-plane: $\vec r \,'= R \left( \begin{array}{c} \cos \phi \cos \theta \\ \cos \phi \sin \theta \\ \sin \phi \end{array} \right)$ with the angle $\theta = \omega t$ in the xy-plane, which takes values ​​from $0^\circ$ to $360^\circ$ over a day. The vector $\vec r$ in the inclined reference system is obtained by multiplication by a corresponding rotation matrix $\vec r = \left( \begin{array}{ccc} \cos \psi & 0 & \sin \psi \\ 0 & 1 & 0 \\ - \sin \psi & 0 & \cos \psi \end{array} \right) \cdot \vec r\,' = \left( \begin{array}{c} \cos \psi \cos \phi \cos \theta + \sin \psi \sin \phi \\ \cos \phi \sin \theta \\ - \sin \psi \cos \phi \cos \theta + \cos \psi \sin \phi \end{array} \right)$ The boundary between day and nigth is at $x= 0$ , so that $\begin{aligned} 0 &= \cos \psi \cos \phi \cos \theta + \sin \psi \sin \phi \\ \Rightarrow \quad \theta &= - \arccos\left[ \tan \psi \tan \phi \right] \approx \pm 60^\circ \end{aligned}$ Therefore, the arc on the day side has a total angle of $\Delta \theta = 120^\circ$ , s.d. the daytime results to $\Delta t = \frac{\Delta \theta}{360^\circ} 24\,\text{h} \approx 8 \,\text{h}$

This problem can be solved with simple 2d trigonometry. In order to solve it, we will look at two cross sections of the earth. The first is a side view, it passes through the center of the earth and the poles, and is perpendicular to the plane which forms the day/night divide.

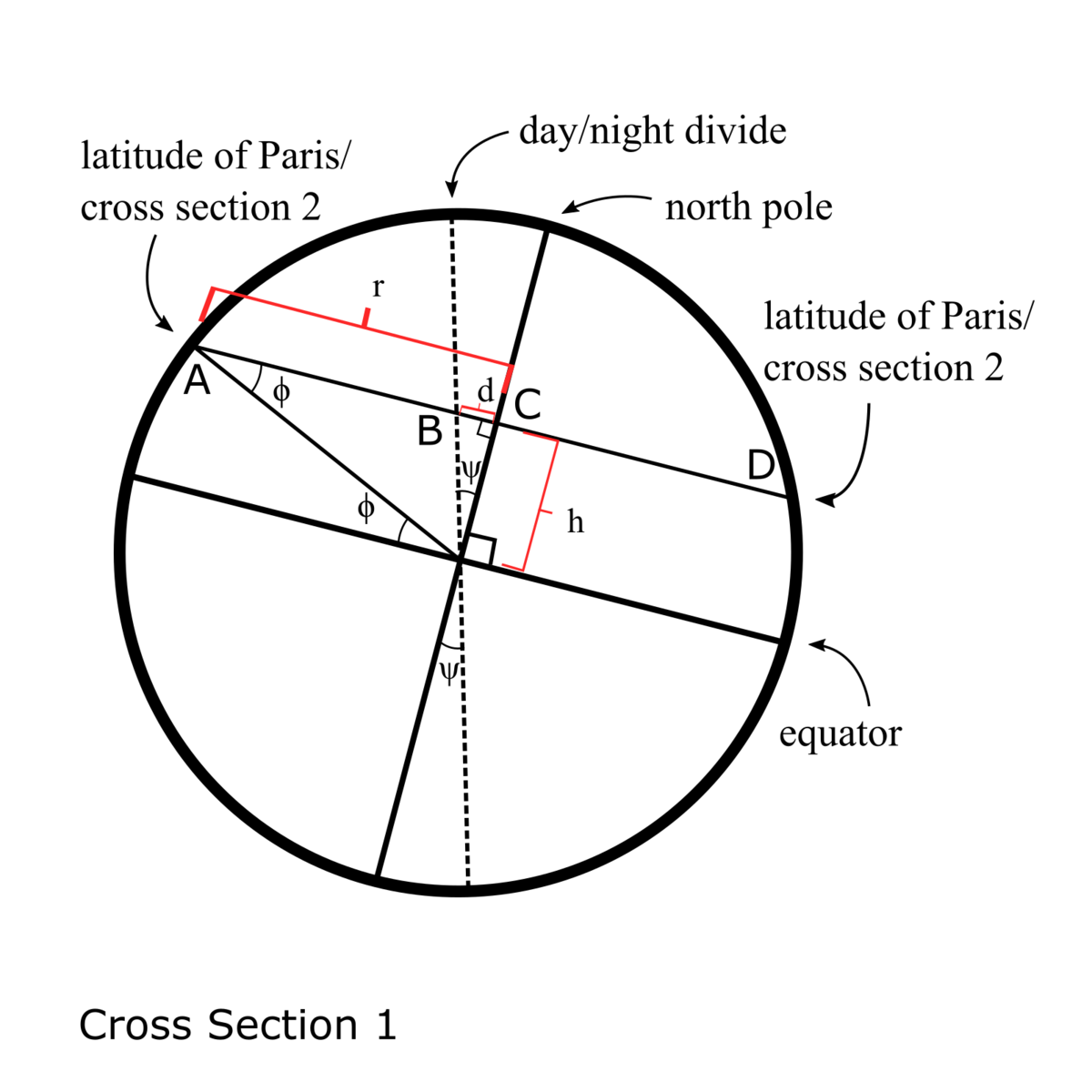
The second cross section passes through the entire latitude that Paris is on. It is perpendicular to the first cross section. The following image is the view from above. Note that the points A, B, C, and D in the first cross section are the same as points A, B, C, and D in the second cross section.

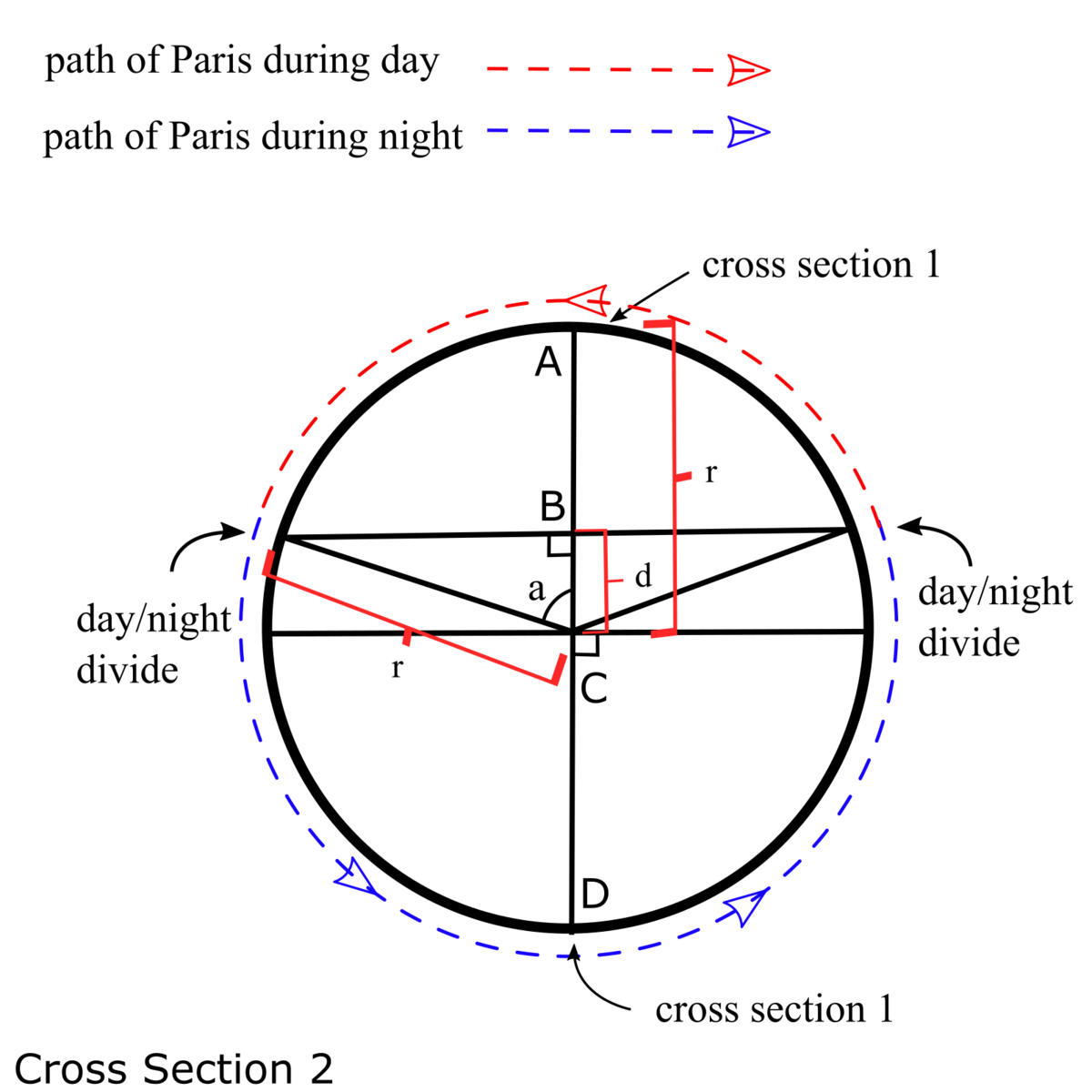
From here, we can use trigonometry to find the angle 'a'.

From the first diagram:

$\frac{d}{h}$ = tan ψ (1)

$\frac{h}{r}$ = tan ϕ (2)

Multiplying (1) and (2) we get:

$\frac{d}{r}$ = tan ψ tan ϕ

From the second diagram:

cos a = $\frac{d}{r}$ = tan ψ tan ϕ

a = arccos(tan ψ tan ϕ)

= arccos(tan 23.4° tan 49°)

= 60.14°

The angle that Paris travels through during the day is 2a or 120.29°.

So, the ratio of the amount of time Paris spends in the sun to the amount of time during a complete revolution of the earth is $\frac{120.29°}{360°}$

The length of the day in Paris is the above ratio multiplied by 24 hours. $\frac{120.29°}{360°}$ * 24 = 8.02 hours

I considered a sphere of radius 1 centered at the origin with the y-axis the axis of rotation. Then I drew a plane through the origin and perpendicular to the xy-plane that formed an angle $\psi$ counterclockwise from the positive y-axis to represent the division line of the half light and half dark side (call it plane 1). Then I drew another plane perpendicular to the xy-plane and parallel to the x-axis that crossed the point $(0,\sin{\phi},0)$ , which contains the circle that Paris lies on (call it plane 2). The intersection of these two planes with the xy-plane form a diameter and a chord (resp.) of the circle that is given by the intersection of the sphere and the xy-plane. Next, I found the equation of plane 1, which was $y=-(\cot{\psi})x$ ; then found the equation of plane 2, which was $y=\sin{\phi}$ . Setting them equal allowed me to find the x-value of the intersection point: $x=-\sin{\phi}\tan{\psi}$ . Next, form a 2-D coordinate system within plane 2 with its origin at its intersection with the y-axis, call its axes u and v, and make them parallel to the x- and z-axes respectively. Scale the axes so that the proportion of any distance measured by the x- or y-axis and that same distance measured by the u- or v-axis is $\cos{\phi}$ . The intersection of plane 1 and plane 2 is a line that lies entirely in the uv-plane. The equation of this line is given by $u=\frac{-\sin{\phi}\tan{\psi}}{\cos{\phi}}=-\tan{\phi}\tan{\psi}$ (division by $\cos{\phi}$ is due to the difference in scale). Likewise, the intersection of the sphere with the uv-plane is a circle of radius 1 centered at the origin. The goal now is to find the distance along the circle that lies to the left of the line (the bright side), and determine what proportion of the entire circle it is. Using the arc length formula from calculus, the distance can be given by $2\int_{-1}^{-\tan{\phi}\tan{\psi}}\sqrt{1+\frac{u^2}{1-u^2}}du=2\int_{-1}^{-\tan{\phi}\tan{\psi}}\frac{1}{\sqrt{1-u^2}}du=2[\arcsin{u}]_{-1}^{-\tan{\phi}\tan{\psi}}\approx 2.0995$ . Dividing this by $2\pi$ , and multiplying by $24$ (hours in a day), I get $8.0193$ hours.

I live at the same latitude. I just aproximatively calculated sunset - sunrise at that time period. I'm a lazy person but result is correct, so I don't care.

I "cheated". Since I live in a city a short-ish distance north of 49° latitude and I know from direct experience that daylight here is on the high side between 7 and 8 hours on the winter solstice, I used my intuition about how far it actually is to 49° from here and concluded that 8 was the most reasonable answer. Of course, that's not mathematically rigorous. However, direct experience with a real world problem is something you risk when posing a real world problem. Of course, I knew I could apply some geometry and trigonometry to the problem but I figured why should I do that when I don't have to?