Wire Frame Cube Moment
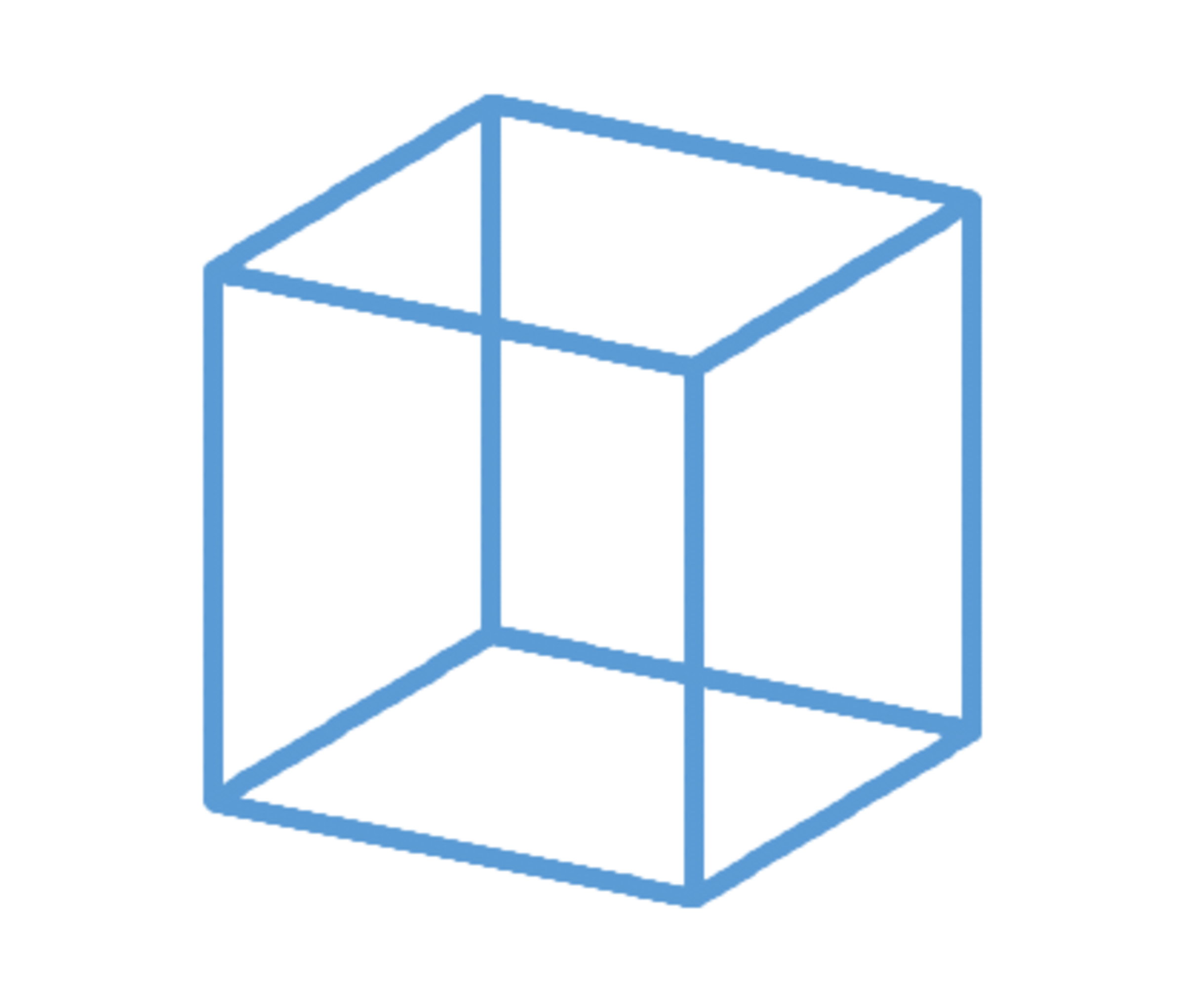
A cubic wire frame consists of 12 segments interconnecting 8 vertices. The vertices are located at the following points:
The wire frame has a mass which is uniformly distributed over its constituent line segments. The object's moment of inertia with respect to an axis perpendicular to the -plane and passing through the point can be expressed as , where and are coprime positive integers.
Determine .
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
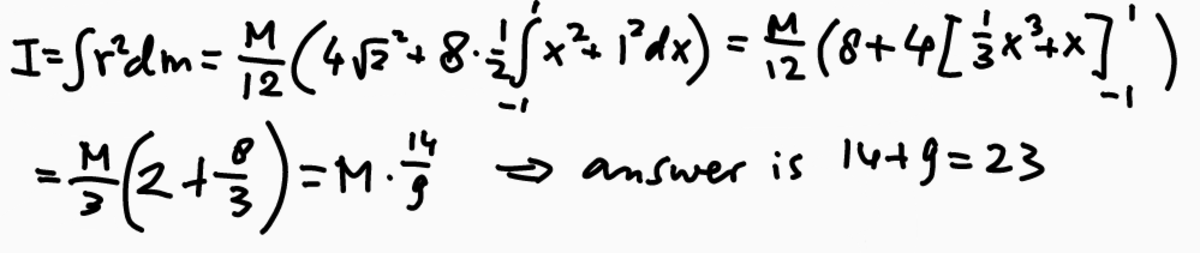
Each of the 12 constituent line segments has a mass 1 2 M and a length of 2. The 8 segments located at either ( z = 1 ) or ( z = − 1 ) can all be treated the same way. Using the Parallel Axis Theorem (since the center of each segment is 1 unit away from the origin) and the expression for the moment of inertia for a rod about its middle ( 1 2 M l 2 ) , the moment for each of these 8 segments is:
1 2 M ∗ 1 2 2 2 + 1 2 M ∗ 1 2 = 3 6 M ∗ 3 6 3 M = 9 M
The moment for the 8 segments is therefore 9 8 M
The remaining 4 segments all have the entirety of their mass located a distance of 2 from the origin, so we can simply use the m r 2 formula for those. The combined moment of inertia for those 4 segments is:
4 1 2 M ( 2 ) 2 = 1 2 8 M = 3 2 M = 9 6 M
The total moment is therefore 9 8 M + 9 6 M = 9 1 4 M = b a M .
( a + b ) = 2 3