Wire Hive
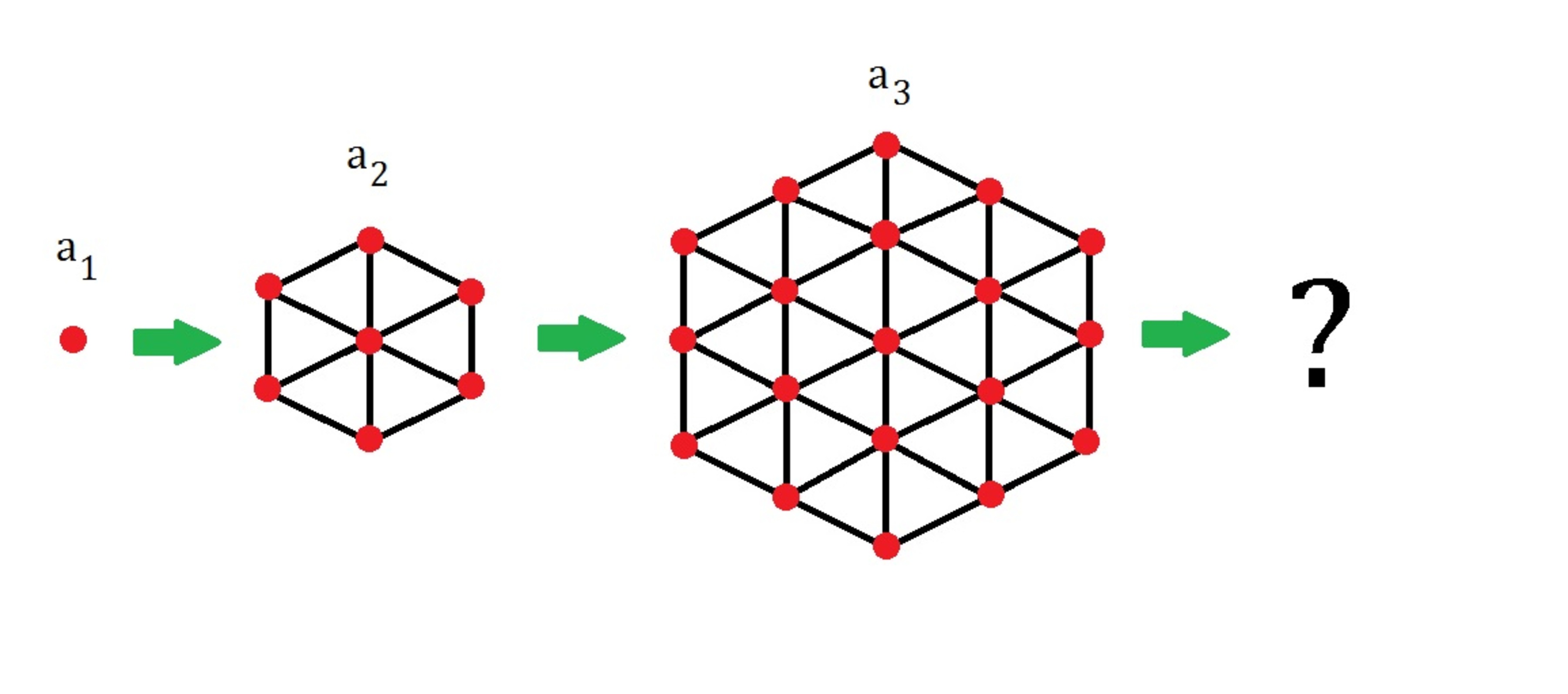
Let be the number of nodes (red) in the enlarging hive-like structure connecting the nodes in sub-units of equilateral triangles as shown above. For instance, ; ; ; etc.
Starting with as the first perfect square, find the next perfect square value of .
The answer is 169.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
a 1 = 1
a 2 = 1 + 6
a 3 = 1 + 6 + 6 × 2
⋮
a n = 1 + 6 × ( 1 + 2 + 3 + ⋯ ) = 1 + 6 × ( 2 n ( n − 1 ) ) = 1 + 3 n ( n − 1 ) = 3 n 2 − 3 n + 1
Suppose a n = m 2 for some integer m .
Then a n = 3 n 2 − 3 n + 1 = m 2 .
3 n 2 − 3 n + ( 1 − m 2 ) = 0
Solving for n , n = 2 × 3 3 ± 3 2 − 4 ( 3 ) ( 1 − m 2 ) = 2 × 3 3 ± 3 ( 3 − 4 ( 1 − m 2 ) ) = 2 × 3 3 ± 3 ( 4 m 2 − 1 ) = 2 × 3 3 ± 3 ( 2 m + 1 ) ( 2 m − 1 )
Considering the discriminant, 3 ( 2 m + 1 ) ( 2 m − 1 ) is a perfect square, and since 2 m + 1 and 2 m − 1 have absolute difference of 2 , they are coprime odd numbers. That means, either 2 m + 1 or 2 m − 1 is a perfect square while the other is a multiple of 3 and another perfect square.
For the latter, the least number is 3 = 3 × 1 2 while the other number is 1 , a perfect square. Plugging in these, we will get n = 1 and a 1 = 1 , which is our first perfect square.
Then the next possible odd multiple is 2 7 = 3 × 3 2 , and then clearly 2 5 = 5 2 , where 2 7 − 2 5 = 2 . Hence, 2 m + 1 = 2 7 ; m = 1 3 .
As a result, the next perfect square is a 8 = 1 3 2 = 1 6 9 .