Without Integration

The integral is $\int_0^{\sqrt{2\pi}}\sin(x^2)\,dx \; = \; \int_0^{2\pi} \frac{\sin u}{2\sqrt{u}}\,du \; = \; \tfrac12\int_0^\pi \left(\frac{1}{\sqrt{u}} - \frac{1}{\sqrt{u+\pi}}\right)\,\sin u\,du \; > \; 0$

Method 1: Without integration. Plotting $y=\sin (x^2)$ from $0$ to $\sqrt{2\pi}$ clearly shows that the curve have a net area under the curve greater than 0 ,

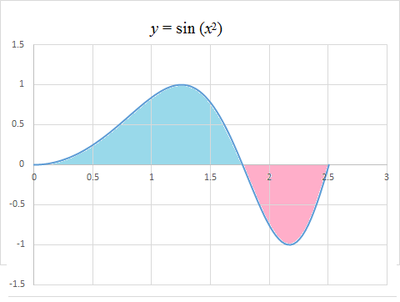
Method 2: With simple integration.

$\begin{aligned} I & = \int_0^{\sqrt{2\pi}} \sin \left(x^2\right) dx & \small \color{#3D99F6} \text{By Maclaurin series} \\ & = \int_0^{\sqrt{2\pi}} \left(x^2 - \frac {x^6}{3!} + \frac {x^{10}}{5!} - \cdots \right) dx \\ & > \int_0^{\sqrt{2\pi}} x^2 \ dx = \frac {x^3}3 \ \bigg|_0^{\sqrt{2\pi}} \boxed {> 0} \end{aligned}$

As Fresnel S is always positive for arguments greater than 0 and 0 at 0. the problem's answer is also greater than 0.

$\sqrt{\frac{\pi }{2}} S(2)$