Wobbly Wobble
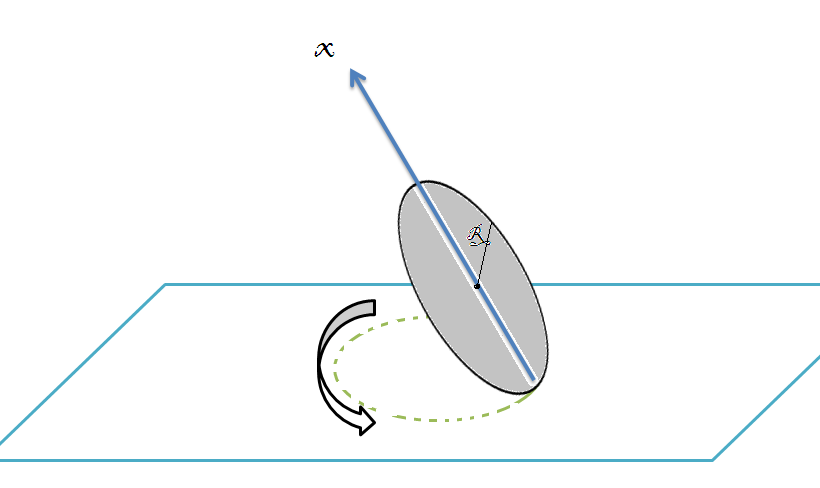
If you spin a coin around a vertical diameter on a table, it will slowly lose energy and begin a wobbling motion. The angle between the coin and the table will gradually decrease, and eventually, it will come to rest.
Assume that this process is slow, and consider the motion when the coin makes an angle with the table. You may assume that the center of mass is essentially motionless. Let be the radius of the coin, and be the frequency at which the contact point on the table traces out its circle. Assume that the coin rolls without slipping.
The angular velocity of the coin is , where points upward along the coin, directly away from the contact point. If and are integers, then, find ,.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
ω = Ω z ^ − ω ′ y ^ = Ω ( s i n θ x ^ + c o s θ y ^ ) − Ω c o s θ y ^ = Ω s i n θ x ^
In retrospect, it makes sense that ω must point in the \hat{x} direction. Both the CM and the instantaneous contact point on the coin are at rest, so ω must lie along the line containing these two points, that is, along the x ^ axis.
The principal moment around the x ^ axis is I = 4 m R 2 . The angular momentum is L = I ω x ^ , so its horizontal component has length L ⊥ = L c o s θ = ( I ω ) c o s θ x ^ . Therefore, d t d L has magnitude
∣ ∣ d t d L ∣ ∣ = Ω L ⊥ = Ω 4 m R 2 ( Ω s i n θ ) c o s θ
and points out of the page.
The torque (relative to the CM) is due to the normal force at the contact point. This normal force is essentially equal to mg, because the CM is assumed to be falling very slowly. Note that there is no sideways friction force at the contact point, because the CM is essentially motionless. The torque therefore has magnitude
∣ τ ∣ = m g R c o s θ and it points out of the page.we finally get, ω = 2 ( R s i n θ ) g