Wood Hunting

Classical Mechanics Level 2

An archer shoots an arrow from his bow with an initial velocity of 100 meters per second. It strikes a wooden block with a mass of 5 kilograms on the edge of a table a short distance away. The arrow sticks in the block, and the block/arrow combination fall off the table and onto the ground, falling a distance of 1 meter. The arrow, which weighed 20 grams, (.02 kg) was fired parallel to the ground, ignored air resistance, and was perfectly balanced throughout. With what horizontal velocity did the block leave the table after impact? (Round to the nearest whole number)

5 m/s 7 m/s 6 m/s 8 m/s

Anthony Sakowski by Anthony Sakowski , 19, USA

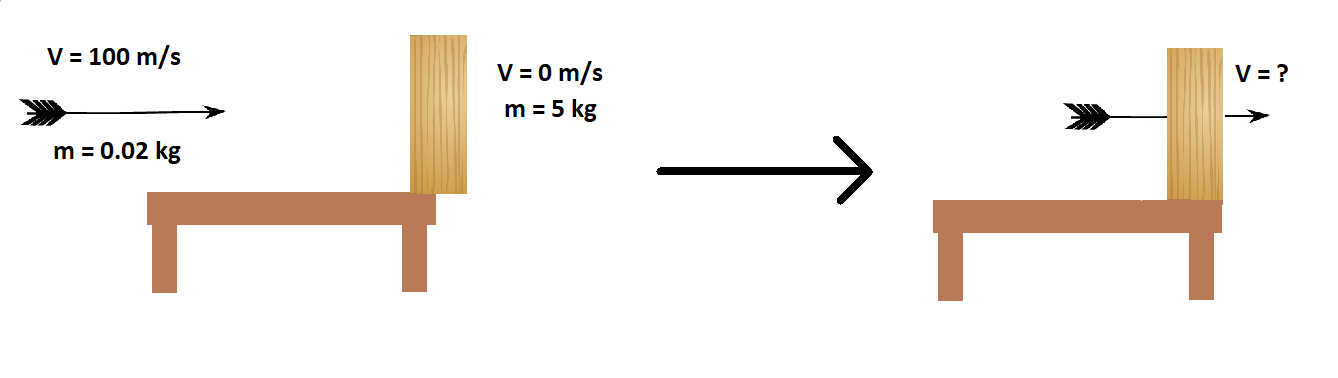
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Michael Mendrin
Oct 10, 2018

In an inelastic collision, energy is not conserved, but momentum is. The answer is far less than any of the multiple choices.

See Inelastic collision

Let m 1 m_1 be the mass of the arrow, m 2 m_2 be the mass of the target, v 1 v_1 the velocity of the arrow, and v 2 v_2 the velocity of the target plus arrow. Then

v 2 = m 1 v 1 m 1 + m 2 ≈ 0.4 v_2 = \dfrac{m_1 v_1}{m_1 + m_2} \approx 0.4 meters per second

0 Helpful 0 Interesting 0 Brilliant 0 Confused

How'd you end up solving it then, if all the answer choices are bogus?

Steven Chase - 2 years, 8 months ago

Log in to reply

I assumed that kinetic energy is conserved, which is not the case. It's momentum that's conserved, not kinetic energy, in case of inelastic collisions such as this. I used this formula, which is erroneous

1 2 m 1 v 1 2 = 1 2 ( m 1 + m 2 ) v 2 2 \frac{1}{2}m_1 v_1^2 = \frac{1}{2} (m_1 + m_2) v_2^2

to find v 2 v_2 which works out to about 6.3 6.3 meters per second

If this was really true, then small bullets fired from guns would be knocking over people like how it is in the movies. If a 45 caliber bullet weighs about 1/30 of a pound, and is fired at about 800 feet per second, when a 150 pound person is hit with it, then according to this bogus equation, the person is sent flying at about 12 feet per second. Yeah, just like how it is in the movies. In fact, the answer is closer to about 2 inches per second.

Michael Mendrin - 2 years, 8 months ago

1 pending report

Vote up reports you agree with

×

Problem Loading...

Note Loading...

Set Loading...