Work Done by Force Field (Part 4)
A particle in the x y -plane is acted upon by a force field described by the equation below: F = ( 2 3 x − 2 1 y ) ı ^ + ( 2 1 x + 2 3 y ) ȷ ^ . How much work does the force field do on the particle if the particle makes one complete revolution over a unit circle centered on the origin?
Notes: ı ^ and ȷ ^ denote unit vectors in the x and y directions, respectively. Give your answer as a positive number to 2 decimal places.
The answer is 3.14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Where S is the unit disk. Nice approach!
On the unit circle we have x = cos ( θ ) and y = sin ( θ ) . So the components of the given force are
F i = 2 3 cos ( θ ) − 2 1 sin ( θ ) = cos ( 6 π ) cos ( θ ) − sin ( 6 π ) sin ( θ ) = cos ( θ + 6 π ) and
F j = 2 1 cos ( θ ) + 2 3 sin ( θ ) = sin ( 6 π ) cos ( θ ) + cos ( 6 π ) sin ( θ ) = sin ( θ + 6 π ) .
Now on the unit circular path C with r = < cos ( θ ) , sin ( θ ) > the work done by F is
W = ∫ C F ⋅ d r = ∫ 0 2 π F ⋅ d θ d r d θ =
∫ 0 2 π < cos ( θ + 6 π ) , sin ( θ + 6 π ) > ⋅ < − sin ( θ ) , cos ( θ ) > d θ =
∫ 0 2 π ( − cos ( θ + 6 π ) sin ( θ ) + sin ( θ + 6 π ) cos ( θ ) ) d θ =
∫ 0 2 π sin ( ( θ + 6 π ) − θ ) d θ = ∫ 0 2 π sin ( 6 π ) d θ = 2 1 × 2 π = π = 3 . 1 4 to 2 decimal places.
Nice use of trig identities. I wasn't quite sure how hard it would be to go from start to finish. In making the problem, I went from "finish" to "start". We've seen one where F is at a right angle with the path, yielding zero net work. We've also seen one where F is perfectly aligned with the path, yielding 2 π as a result. If they were 60 degrees apart, that would give us a factor of c o s ( 6 0 ∘ ) = 2 1 , yielding a final value of π . So to get that, just shift the force by 30 degrees, starting with the radial configuration. Using complex numbers ( j = − 1 ) to make sense of the arithmetic of multiplying vectors yields:
F = ( x + j y ) ( 2 3 + j 2 1 ) = 2 3 x − 2 1 y + j ( 2 1 x + 2 3 y )
Converting back into unit vector form gives:
F = ( 2 3 x − 2 1 y ) ı ^ + ( 2 1 x + 2 3 y ) ȷ ^ .
If we rotate the system by 60°,the force equation would yield F=-yî+xj which is a force of magnitude 1 for a unit circle path,hence the torque being T=FR=1Nm! The work should then be T*@=2π shouldn't it be??
Log in to reply
In my approach, I rotated the force by 30 degrees relative to the radial direction. So it's now at 60 degrees with respect to the motion, giving us a factor of c o s ( 6 0 ∘ ) = 2 1 . If we rotated the force 60 degrees relative to the radial direction, the force would be at 30 degrees with respect to the motion, giving a factor of c o s ( 3 0 ∘ ) = 2 3 . So we would have 3 π .
With the force field you specify, we would indeed get 2 π . But that would come from a 90 degree rotation of the force field with respect to the radial. I've actually posted that very problem. It was Part 1, I believe.
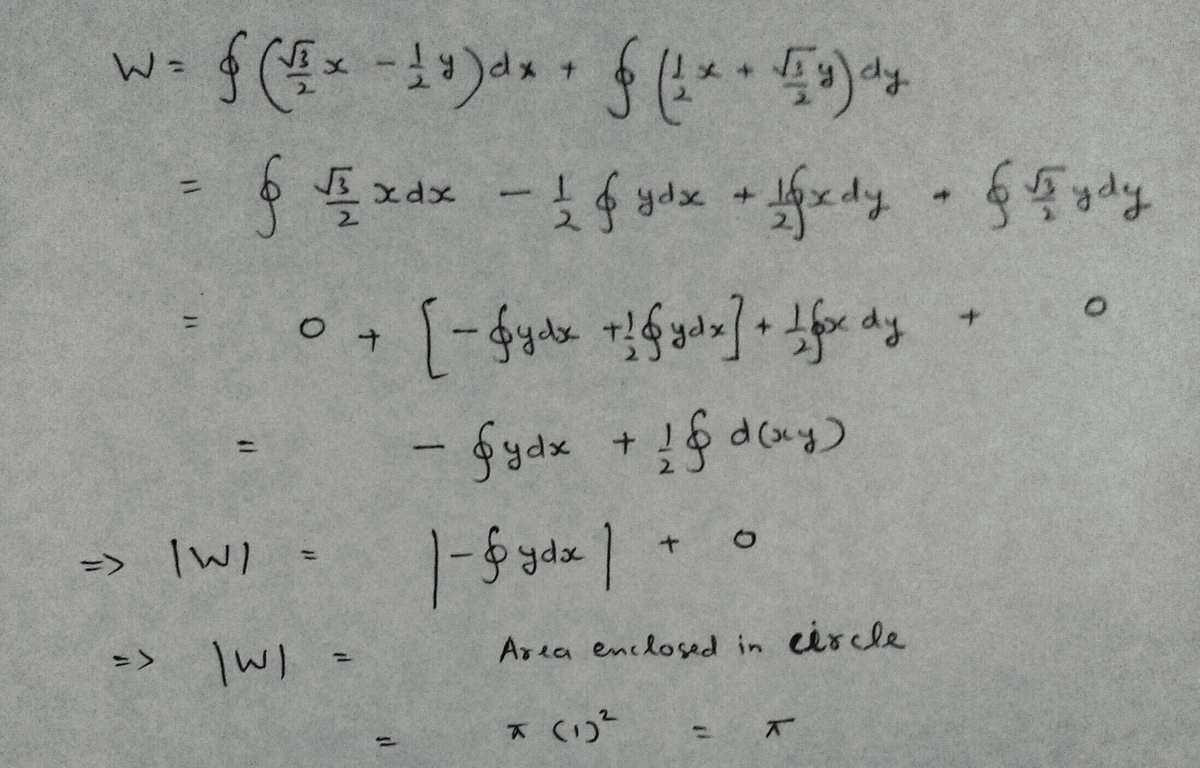
Using the Kelvin-Stoke's theorem, we have ∮ F ⋅ d l = ∫ ∇ × F ⋅ d S = ∫ 1 d S = π .