Work done on a superconductor
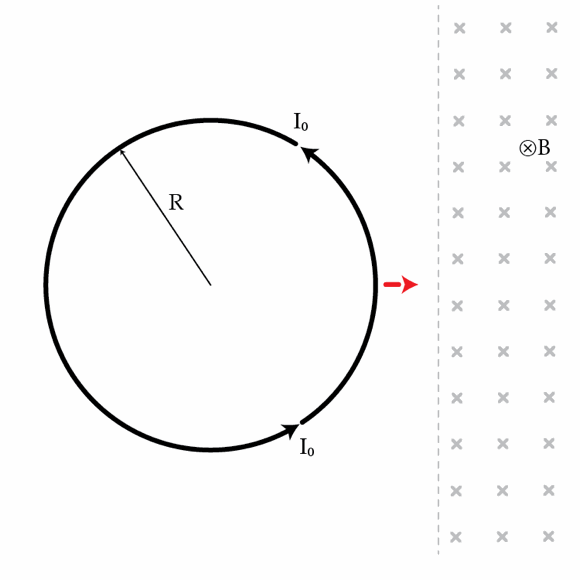
A superconducting (zero resistance) ring of radius
R
=
2
cm
and self inductance
L
=
0
.
5
nH
is located in a region of zero magnetic field. A current
I
0
=
0
.
1
A
circulates around the ring as shown in the figure below. What minimum work
in Joules
must be done on the ring to fully immerse it in a region with a uniform magnetic field
B
=
0
.
1
T
(directed into the page)?
The answer is 15.79.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Because the ring is superconducting, the magnetic flux through the ring must be constant.
Therefore, the external magnetic field will increase the current circulating around the ring by: Δ I = L B S = L B π R 2 = 2 5 1 2 0 0 ( A ) .
We notice that Δ I is by far bigger than I 0 , so we can exclude I 0 when calculate the work needed to move the ring: A = Δ W = 2 L Δ I 2 = 1 5 . 7 9 ( J )
Since this is a superconducting ring, we may write the equation as below:
B d t d A = L d t d I
B Δ A = L Δ I
Δ I = L B Δ A
Δ I = L B π R 2
Since its minimum work denotes by E = 2 1 L ( Δ I ) 2 ,
E = 2 L B 2 π 2 R 4
E = 2 × 0 . 5 × 1 0 − 9 ( 0 . 1 ) 2 × π 2 × ( 2 × 1 0 − 2 ) 4
E = 1 5 . 7 9
If the ring is 'x' into the field, as shown:

If the sector makes angle 'q', Area of sector = r^2 * q/2 Area of triangle = r^2 * sin(q)/2 Hence, area in magnetic field = (r^2 / 2) (q - sin(q)) Flux linkage = B A = B r^/2 * (q - sin(q)) EMF generated = d(Flux linkage)/dt = (B r^2/2) * (dq/dt) * (1-cos(q)) This is opposed by inductance = L di/dt => (B r^2/2) * (1-cos(q)) * dq/dt = L di/dt dt will get cancelled (B r^2/2) * (1-cos(q)) * dq= L di Integrating both sides: LHS: angle changes from 0 to 2 pi. (B r^2/2) (2 pi - 0) = L del i => L* del i = B pi r^2
del_i = (B pi r^2 / L)
Energy change: (0.5 * L * (I0 + del_i)^2 - 0.5 * L * I0^2) = 15.7914 J
By immersing the ring in the region with the magnetic field, there will be an increase in the magnetic flux through the ring into the page. Then, by Lenz's law, there will be an induced e.m.f which could result in a counter-clockwise current (i.e., in the same direction as the 0 . 1 A current) to counteract the change in the magnetic flux.
However, since the ring is superconducting, we cannot allow this induced e.m.f. to occur, otherwise the resultant current will be infinite, which violates the law of conservation of energy. Thus, there should be another e.m.f. produced that cancels out the induced e.m.f.; this e.m.f. produced comes from the inductance of the ring. Hence, we have the equation below:
B d t d A = L d t d I ⇒ B Δ A = L Δ I
Since we know that Δ A is simply the area of the ring, we can find Δ I . However, the main point here is that there is a change in the current flowing through the ring. Then, since we know that the stored energy in an inductor is given by
E = 2 1 L I 2
the increase in the magnitude of the current must mean that more energy is stored in the ring after it has been immersed in the magnetic field. This must mean that there is an input of energy into the system. Letting the initial current of 0 . 1 A be I 0 , this input energy is simply
Δ E = 2 1 L [ ( I 0 − Δ I ) 2 − I 0 2 ]
We get 1 5 . 7 9 J