Work of Lawn mower
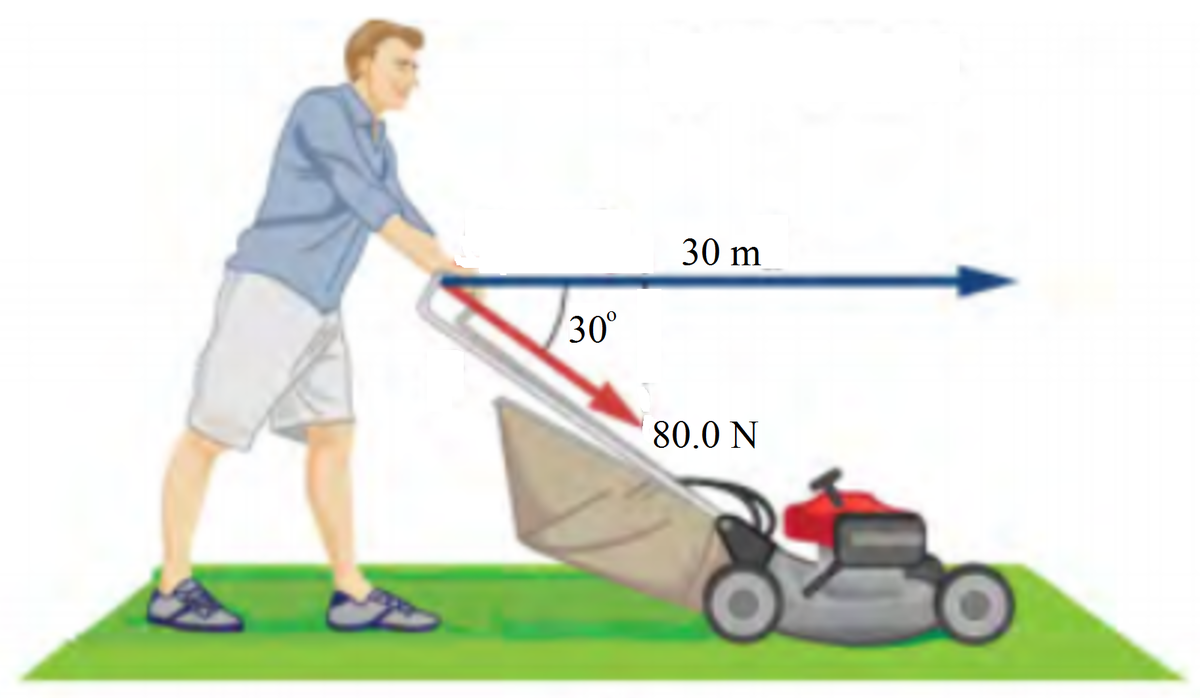
How much work is done on the lawn mower by a person, if he exerts a constant force of 8 0 . 0 N at an angle 3 0 ∘ below the horizontal and pushes the mower 3 0 . 0 m on level ground? Answer in joules correct to two decimal places.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
We're looking for the x component of the work done by the person onto the lawnmower. The formula for work is W = F d . In this problem, we'll be looking for the x component of the work, so we'll be using the formula W x = F x ⋅ x , where x is the horizontal distance over which the person pushes the lawnmower forward ( x = 3 0 m ) .
In the image below, the red rectangle is the lawnmower. The force applied by the person is F a p p l i e d . F x is the x component of the force he applies on the lawnmower, and F y is the y component of the person's force (neglecting the force of gravity, since we only care about the force applied by the person).
 The image below shows the equations for the
x
and
y
components of the applied force. We're only concerned with the x component, so we'll need to solve the blue equation for the x component of the force the person applies onto the lawnmower.
The image below shows the equations for the
x
and
y
components of the applied force. We're only concerned with the x component, so we'll need to solve the blue equation for the x component of the force the person applies onto the lawnmower.

F x = 8 0 cos 3 0 ∘ = 8 0 2 3 = 4 0 3 N
Now that we know F x and x , we can solve for W x :
W x = ( 4 0 3 N ) ( 3 0 m ) = 1 2 0 0 3 J ≈ 2 0 7 8 . 4 6 J .
W = F . d . cos μ J o u l e s
W = 8 0 × 3 0 × cos 3 0 ° J o u l e s
2 0 7 8 . 4 6 J o u l e s