Work on Planet Brilliant
A 3D model of Brilliant's logo has found itself on Planet Brilliant, whose dimensions and gravitational force is unknown. Starting from rest at the top of the hill, the ball rolls down a hill peaking at 10 meters from ground-level (whose slopes are frictionless) and is en route to a path with a frictional co-efficient of 0.5. How far does the model travel along the ground until it comes to a stop?
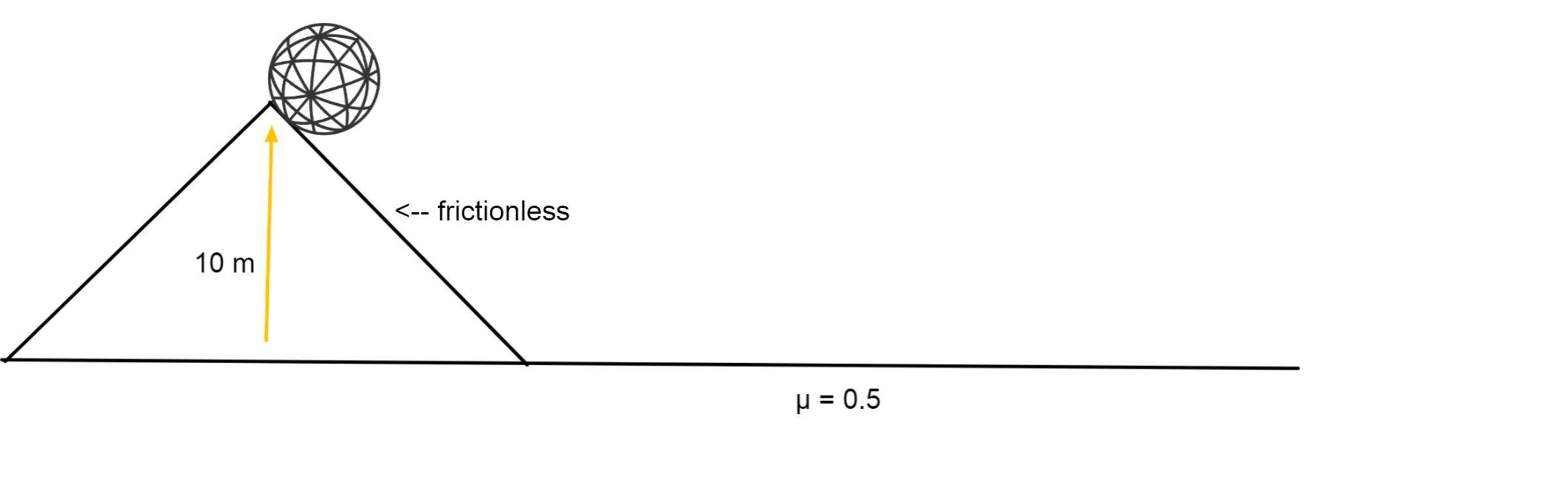
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The ball will continue moving until it reaches ground level, where energy is dissipated due to frictional force. The energy the ball had at first will hence equal to the energy the ground takes from it, which means that the gravitational potential energy of the ball will equal to the resisting work done by the ground.
m g h = μ N d m g h = μ × m g × d h = μ d 1 0 = 0 . 5 × d
d = 0 . 5 1 0 = 2 0