Work Outwards!
An equilateral triangle is inscribed in a circle. If the area of the triangle is 4 8 3 , the area of the circle can be expressed as x π , where x is a positive integer.
Submit the value of x .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Just use a/sin(A) = 2R
Log in to reply
yeah that's one way of doing it... I used the sine rule because I think more people are familiar with it
Just divide the figure into 3 equal parts thru' the centre.
The angle at centre of each sector is 1 2 0 ° and the pink area = 1 6 3
2 1 r 2 sin ( 1 2 0 ° ) = 1 6 3 ⟹ r 2 = 6 4
Divide the triangle into 6 identical right triangles. The radius
r
bisects the
6
0
∘
angles of the equilateral triangle.
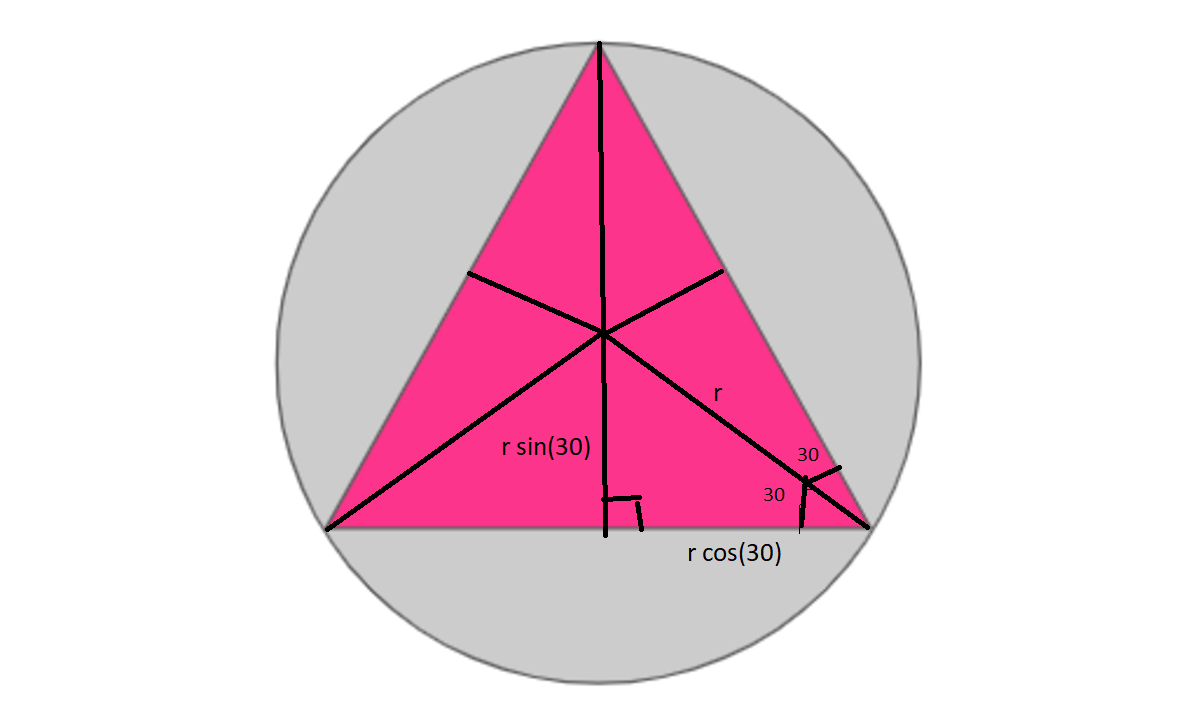
The area of one of these right triangles is 6 4 8 3 = 8 3 . We can solve for the radius of the circle using this quantity. 2 1 ⋅ r cos ( 3 0 ) ⋅ r sin ( 3 0 ) = 2 1 ⋅ 2 3 r ⋅ 2 r = 8 3 r 2 = 8 3 r 2 = 6 4 Therefore, the area of the circle is A = π r 2 = 6 4 π
Nice approach 😎
There are multiple methods to solve this problem, feel free to upload your solutions!
The side of the triangle (i.e. A C and the other 2 sides) is 8 3 cm (This can be found very easily, for example using 2 1 a b sin c or other methods).
Now let's focus on Triangle A B C , where point B is the center of the circle. It is isosceles since A B and B C are radii of the circle. If we find the length of A B or B C , then we can just find the area of the circle.
Since ∠ A B C = 1 2 0 ∘ , we have a side and an opposite angle, therefore by using the sine rule in a triangle we get:
sin 1 2 0 8 3 = sin 3 0 r where r is the radius of the circle.
We get r = 8 . Therefore the area of the circle is 6 4 π .
The answer is 6 4 .