Work Power Energy
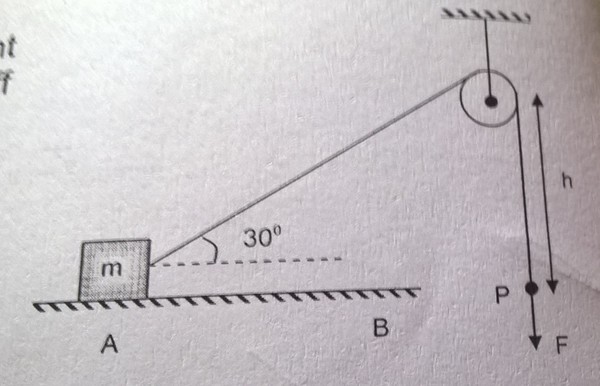
A block of mass m is dragged across the smooth floor by the constant force F acting at the end of the rope Assume the block does not lift off the floor. How many of the given statements are correct?
a) Work done by F on the block when the block move from A to B(at B angle made by the string with horizontal is 53 degrees) is 3Fh/4.
b) Work done by F on the block when the block move from A to B(at B angle made by the string with horizontal is 53 degrees) is 3Fh/5.
c) Power delivered by applied force from A to B is .
d) The velocity of point P when the string makes an angle of 37 degrees with the horizontal is .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Here's a bit of work on this problem. Some of these results are a bit curious in relation to the proposed answers, so please comment if you see something wrong. Suppose the horizontal distance between the block and the pulley is x and θ is the angle between the horizontal and the rope.
t a n ( θ ) = x h
Derive an expression for the work done on the block in going between two values of θ .
Horizontal force:
F h = F c o s ( θ )
Differential work:
d W = − F h d x = − F c o s ( θ ) d x
Implicitly differentiate the tangent expression to get an expression for d x in terms of d θ .
s e c 2 ( θ ) d x d θ = x 2 − h = − h t a n 2 ( θ ) d x d θ = − h s i n 2 ( θ ) d x = − s i n 2 ( θ ) h d θ d W = F h s i n 2 ( θ ) c o s ( θ ) d θ
Integrate to get the work done on the block:
W = F h ∫ θ 1 θ 2 s i n 2 ( θ ) c o s ( θ ) d θ = F h ∫ s i n ( θ 1 ) s i n ( θ 2 ) u 2 d u = F h ( s i n ( θ 1 ) 1 − s i n ( θ 2 ) 1 )
The work done between A and B is therefore:
W A B = F h ( s i n ( 3 0 ∘ ) 1 − s i n ( 5 3 ∘ ) 1 ) ≈ 0 . 7 4 7 8 6 F h
Interestingly, this is close to Option (a) but not exactly the same. Option (b) is clearly wrong.
I'm not exactly sure what (c) is asking for, so I'll skip to (d). Equate the work done on the block to the block kinetic energy.
F h ( s i n ( 3 0 ∘ ) 1 − s i n ( 3 7 ∘ ) 1 ) = 2 1 m ( d t d x ) 2 ⟹ d t d x ≈ 0 . 8 2 2 6 3 m F h x = t a n ( 3 7 ∘ ) h ≈ 1 . 3 2 7 0 4 5 h
The speed of point P is equal to the rate of change of the length of rope hypotenuse on the left side of the pulley (call this L ):
L 2 = x 2 + h 2 2 L d t d L = 2 x d t d x d t d L = L x d t d x = x 2 + h 2 x d t d x
Evaluating gives:
x 2 + h 2 x d t d x = 1 + 1 . 3 2 7 0 4 5 2 1 0 . 8 2 2 6 3 m F h ≈ 0 . 6 5 6 9 8 2 m F h
Interestingly again, this is very close to the proposed answer for (d), but not quite the same.