Work those Quadriceps
 Suppose
A
B
C
D
is a cyclic quadrilateral with all integral sidelengths and
A
D
being the circumdiameter. Sides
A
B
and
B
C
both having length
a
and side
C
D
having length
b
such that
a
=
b
.
Suppose
A
B
C
D
is a cyclic quadrilateral with all integral sidelengths and
A
D
being the circumdiameter. Sides
A
B
and
B
C
both having length
a
and side
C
D
having length
b
such that
a
=
b
.
Determine the sum of the 4 smallest possible perimeters of quadrilateral A B C D .
Inspired by this beautiful problem
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The famous whiteboard in action. :)
There is actually another configuration for perimeter 22, which is (6,6,1,9). And another one for perimeter 44 too, which is (12,12,2,18).
Thanks for the excellent problem!
Log in to reply
The problem asks for the sum of the four smallest perimeter lengths possible, regardless if there's more than one solution for a given perimeter length. I blew my first answer because of this.
Log in to reply
I knew, as I did the same thing, counted 22 twice! Then reread the problem and figured out what he meant.
same to me.
Hmm, this makes me think. I never realized just how large values of n could get. For the (6,6,1,9) solution n=16 and for the (12,12,2,18) solution n=32.
If someone could write a code to find the first so many values of each variable that would be great
@Michael Mendrin how did you solve this problem? Did you work it by cases or some other method.
Log in to reply
Notice that I can rearrange the sides so that sides of lengths b and c are parallel. Then using a bit of algebra, we end up with the equation
2 a 2 + c b − c 2 = 0
and so we look for integer solutions for it. It's a bit of tedious to work out enough of them to see that the smallest 2 a + b + c are 1 9 , 2 2 , 3 8 , 4 1 , mainly by looking for a , b such that 8 a 2 + b 2 is a square, which can readily be tabulated. I didn't bother proving to myself that these were the smallest, I simply took a chance in answering this question, hoping that you proved it.
Log in to reply
Ya, working with individual cases and a little bashing will take much less time than doing it the way that I did it. I just wanted to generalize it and completely prove it to find all the lengths possible. Which turns Brian's 1 page solution from his original problem into a 4 page essay.
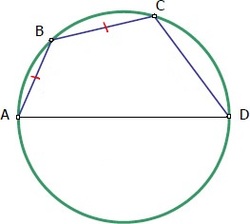
Let O be the centre of the circle, M be the midpoint of A B , and d = A D . Draw the line segments O M , O B and O C . Let θ = ∠ A O M . Then a = A B = 2 M A = 2 O B sin ( θ ) = d sin ( θ ) .
By congruent triangles, we can see that ∠ A O B = 2 θ and ∠ B O C = 2 θ , so ∠ A O C = 4 θ . Now Euclid's Elements III.20 says the angle at the circumference is half the angle at the centre (in other words ∠ A D C = 2 1 ∠ A O C ). Hence ∠ A D C = 2 θ .
Draw line segment A C . By Thales' theorem, ∠ A C D = 9 0 ∘ . Therefore, b = C D = A D cos ( 2 θ ) = d ( 1 − 2 sin 2 ( θ ) ) = d ( 1 − 2 ( d a ) 2 ) = d − d 2 a 2
Hence 2 a 2 is divisible by d . Let's look at a few cases:
a = 1 → d ∣ 2 . Now d can't be 1 since d > a . It also can't be 2 because then we would have b = a . Hence there are no solutions in this case.
a = 2 → d ∣ 8 . Now d = 1 , 2 is too small, and d = 4 leads to a = b . However d = 8 works, giving a solution of ( a , b , d ) = ( 2 , 7 , 8 ) .
a = 3 → d ∣ 1 8 . Here d = 1 , 2 , 3 are too small and d = 6 leads to a = b . However d = 9 , 1 8 work, giving solutions of ( 3 , 7 , 9 ) and ( 3 , 1 7 , 1 8 ) .
a = 4 → d ∣ 3 2 . Here d = 1 , 2 , 4 are too small and d = 8 leads to a = b . However, d = 1 6 , 3 2 give the solutions ( 4 , 1 4 , 1 6 ) and ( 4 , 3 1 , 3 2 ) .
So far the 4 smallest perimeters are 1 9 , 2 2 , 3 8 , 4 1 . All that's left to do is prove that these are the smallest possible perimeters. However, this is a little tedious and 2 other people have already done it, so I'll skip this part.
Hence the answer is 1 9 + 2 2 + 3 8 + 4 1 = 1 2 0 .
Wow. Thanks for this! Truly amazing what you did here and this really helps to show the lengths.
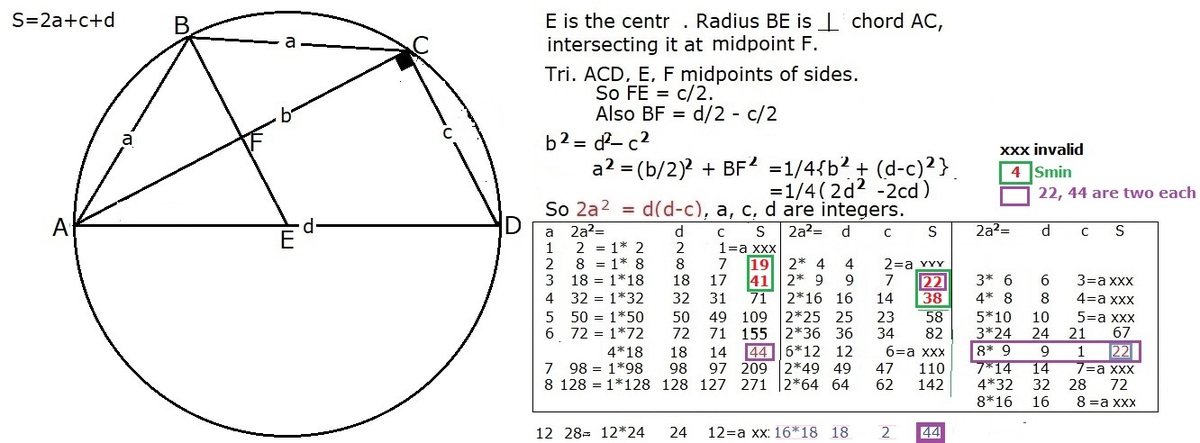

I h a v e g i v e n a f u l l l i s t s o t h a t c h a n g e s i n v a r i a b l e s c a n b e s e e n . F o r t h e s o l u t i o n o f t h i s p r o b l e m t h e r e i s a s h o r t c u t . ( 1 ) A s ′ a ′ i n c r e a s e s , p e r i m e t e r S d e c r e a s e s . ( 2 ) W h e n ( d − c ) = a , a n d d = 2 a , t h e n S = 5 a . ( 3 ) I f t h e r e i s n o f a c t o r m ∗ n , a < m , n < 2 a , S = 5 a i s m i n i m u m S m f o r t h a t v a l u e o f a . ( 3 a ) I f S m > o u r d e s i r e d v a l u e 4 1 , w e e n d o u r i n v e s t i g a t i o n . ( 3 b i ) I f S m ≤ o u r d e s i r e d v a l u e 4 1 , w e g o f o r v a l u e o f ( d − c ) , b e f o r e i t w a s a . ( 3 b i i ) i f T H I S S > 4 1 w e e n d o u r i n v e s t i g a t i o n . ( 3 b i i i ) I f S m ≤ 4 1 , g o f o r v a l u e o f ( d − c ) , b e f o r e . ( 4 ) I f t h e r e i s a f a c t o r m ∗ n , a < m , n < 2 a , t h i s S i s s a m e a s o n e o f t h e S w e s a w , b u t w i t h d i f f e r e n t a , c , a n d d . N e g l e c t .

This solution discusses the method of how to find every cyclic quadrilateral that fits under the given parameters of this question. However, this does make it lengthy and you may wanna skip some of the computations if you like.
Let ∠ C D A = θ . thus by cyclic properties, ∠ A B C = 1 8 0 − θ . Now, using circle theorems, since A D is a diameter ∠ A C D = 9 0 . Finally, let segment A C = x .
By Pythagorean theorem, x 2 = d 2 − b 2
By law of cosines, x 2 = 2 a 2 − 2 a 2 cos ( 1 8 0 − θ ) . Setting the two equal to each other (also note that cos ( 1 8 0 − θ ) = − cos ( θ ) )
d 2 − b 2 = 2 a 2 + 2 a 2 cos ( θ )
Also, remember that b 2 = d 2 cos ( θ ) 2
d 2 − d 2 cos 2 ( θ ) − 2 a 2 ( 1 + cos ( θ ) ) = 0
d 2 ( 1 − cos ( θ ) ) ( 1 + cos ( θ ) ) − 2 a 2 ( 1 + cos ( θ ) ) = 0
( d 2 − d 2 cos ( θ ) − 2 a 2 ) ( 1 + cos ( θ ) ) = 0
Once again, cos ( θ ) = d b
( d 2 − d b − 2 a 2 ) ( 1 + cos ( θ ) ) = 0 ( i )
One of the two equates to 0, obviously 1 + cos ( θ ) = 0 . So using the quadratic we have
d = 2 b ± b 2 + 8 a 2
Note that since d can't be negative, the ± is actually just a + .
Using this formula on integral square roots (a little lemma I made whose properties I have still yet to fully exploit), we obtain the following equation for integral solutions for d and a . Note that the lead coefficient of b here is 1 which is a perfect square.
b = 2 n 8 a 2 − n 2
Where n is an arbitrary variable we will be playing with here. Plugging in this value for b yields
d = 2 2 n 8 a 2 − n 2 + 4 n 2 6 4 a 2 − 1 6 a 2 n 2 + n 4 + 8 a 2
d = 2 2 n 8 a 2 − n 2 + ( 2 n ) 2 ( 8 a 2 + n 2 ) 2
d = n 4 a 2 ( i i )
Going back to equation (i) with our new value of d
d 2 − d b − 2 a 2 ⟶ n 2 1 6 a 4 − n 4 a 2 b − 2 a 2 = 0
⟶ ( 8 a 2 − 2 b n − n 2 ) 2 a 2 = 0
Since a = 0
a = 8 2 b n + n 2
Finally, substituting our value of a from equation (ii) a = 2 d n
2 d n = 8 2 b n + n 2
b = 2 2 d − n
From this final equation, it can be easily observed that n MUST be even for b to be even
We now have all the equations we need to make our cyclic quad under the parameters of the question. They are:
When I finally got this result, I had to tell myself, "Sometimes, it's the small things that are beautiful. Diamonds aren't simply found in a minute" #minecraft (no I don't play this game)
From here, it's a simple plug and chug of a along with even values of n .
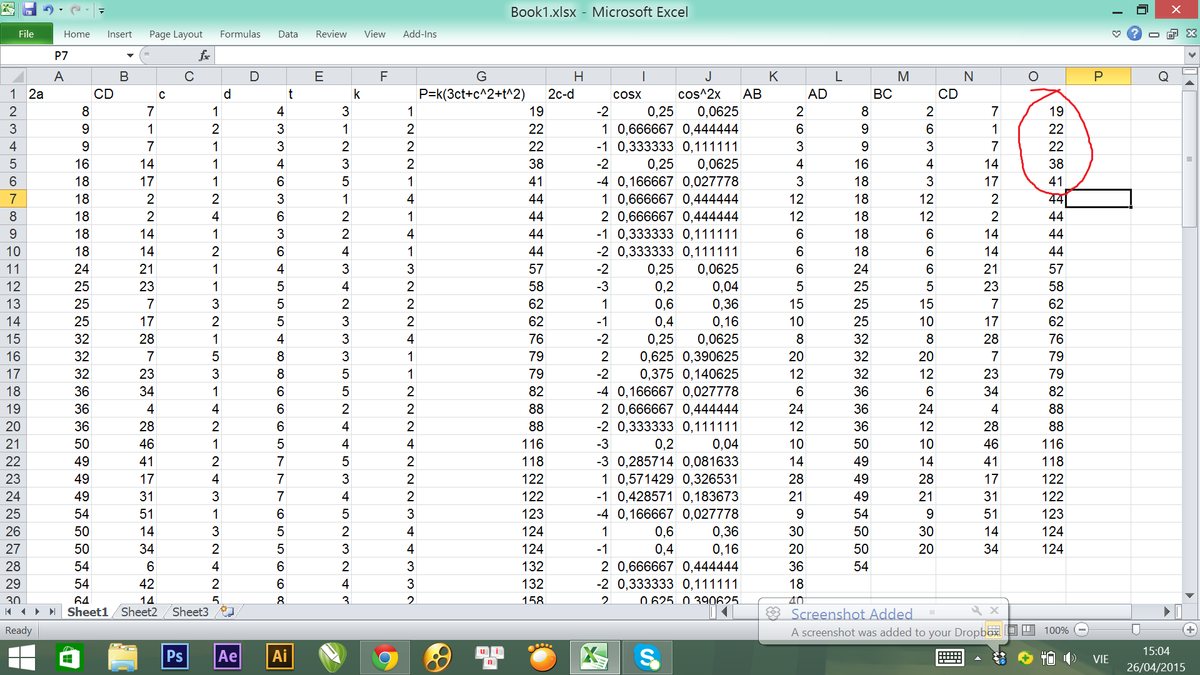
On the chart displayed below. I have a few of the values of a , n , d , b
The 4 smallest values are 1 9 , 2 2 , 3 8 , 4 1
Which have values of
Thus or answer is 1 9 + 2 2 + 3 8 + 4 1 = 1 2 0