The smiling Buddha

Level pending

For each $b \in \mathbb{R}$ , define

$f(b) =\max_{x \in \mathbb{R} } ( |b+sin(x)+\frac{2}{3+sin(x)}|)$

The minimum value of $f(b)$ , is of the form $\frac{s}{t},$ where $s$ and $t$ are coprime integers . Find $s + t$ .

Here $| \cdot |$ denote modulus function and $\max( \cdot )$ denotes the maximum function.

Bonus : A graphical approach to the problem might help you.

The answer is 7.

1 solution

Dhiraj Agarwalla
Nov 29, 2015

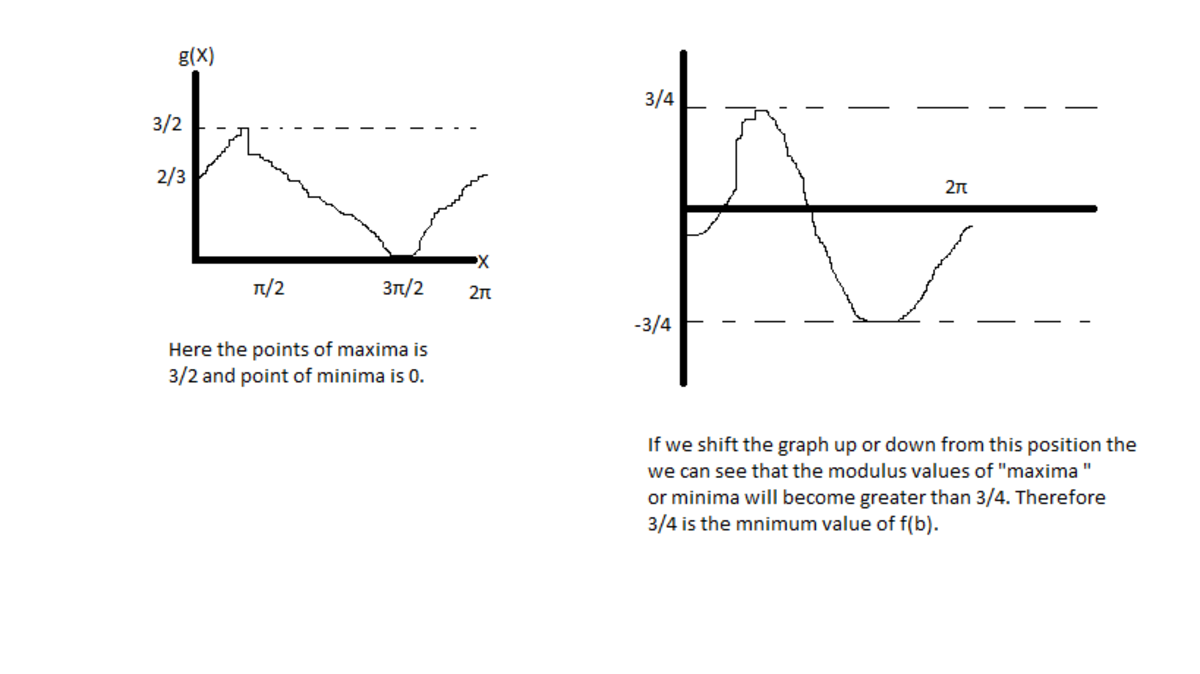
Let $g(x) = sinx + \frac{2}{3+sin(x)}$ . We can see that g(x) is a periodic function of period 2π . We can easily obtain the rough graph of g(x) for the interval [0,2π] using differentiation. If we add any constant to g(x) then the new graph will be simply be the original graph shifted up or down on the y axis . Likewise if we add b to g(x) the graph will shift b units. If some part of the graph goes below x axis then just reflect it on the x axis to get | g(x)+b | . Now finally for a particular b the value of value of f(b) will be the topmost point of the graph |g(x)+b| . Now we can easily see that to get the minimum value of f(b) we need a graph of |g(x)+b| where the topmost point is at the least possible height. So we start to shift the graph of g(x) downwards and we see the height of the topmost point decreases. But at he same time the graph below the x axis starts to come up (because of the modulus function) . If we continue to shift the graph downwards there will come a time where the reflection of the downmost part reaches the same height as that of the topmost part. Further if we shift the graph towards any direction we can see that the height of the topmost point of the graph | g(x)+b| will increase in height. Therefore we reach the conclusion that that particular point is the lowest possible value of f(b) . We can easily calculate the value of that point by dividing the range of the function g(x) by 2. That is $\frac{\frac{3}{2}}{2}$

The smiling Buddha

The answer is 7.

1 solution

0 pending reports