Would Pythagoras be proud?

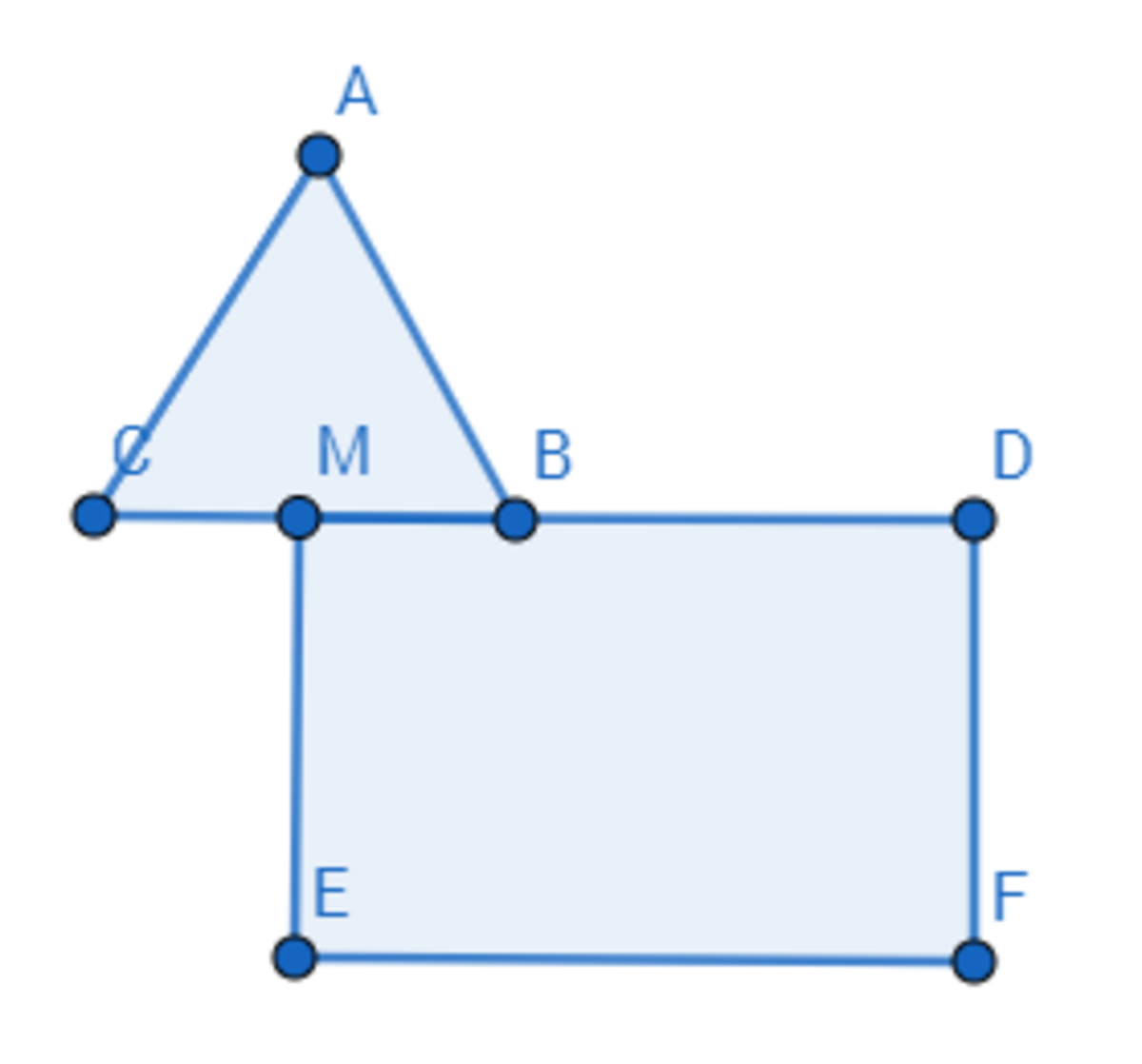
ABC is an equilateral triangle with area 1. The midpoint of BC is M. A rectangle MDEF is drawn so that MD and BC are parallel and MF does not touch C. ME and DF are the diagonals of the rectangle. MD is twice as long as DF. The area of the rectangle is 3. (The shown diagram is not drawn to scale.)

Find the side length of AE.

Express your answer as $\sqrt { \sqrt [ 2 ]{ a } \times \sqrt [ 4 ]{ { b }^{ 3 } } +\sqrt { c } +\frac { d }{ e } }$ , for which $a$ has no square factors (excluding 1) and is a positive integer, $b^{3}$ has no factors which can be written as $k^{4}$ , where k is an integer greater than 1 and for which d and e are coprime positive integers.

Note: This is the most simplified form.

What is the value of $a+b+c+d+e$ ?

Click here for more geometry problems .