Wrap the cube

Logic Level 1

We have a $1\times 1\times 1$ orange cube on a piece of $3\times 3$ blue paper. Is it possible to cover the entire cube with the paper under the following conditions?

The paper can only be cut or folded along the grid.
The cut should not cause the paper to separate into pieces.

Yes, it is possible No, it is not possible

8 solutions

Donnie Adams
May 15, 2017

Cut along the red lines. Then, fold along the dotted lines such that any green line is inside of the fold while any black line is outside of the fold. Every fold should be at a 90° angle except for two, the green fold in the bottom row and the black fold in the right column both of which should be 180°, both sides of the fold flat against one another. If each of the squares in the 3x3 was numbered 1-9, these folds would be between squares 7-8 and 6-9 respectively.

Following these folds properly, the 3x3 paper should be in the shape of a cube, around the center face without the need to move the cube.

Moderator note:

Part of what makes this problem difficult is that the typical mathematical object used to fold a polyhedron is a net , which by definition assumes all adjacent polygons remain joined once the net is folded. None of the typical nets for a cube (one is depicted below) can fit within a 3 by 3 arrangement of squares.

The cutting of adjacent polygons in net-folding is a relatively unexplored avenue of mathematics!

I find this cutting also. Cut between 4 & 5 instead of between 1 & 4.

Guiseppi Butel - 4 years ago

Nice solution! It's easy to miss the fact that the paper can be folded in different directions, and not all folds have to be at 90 $^\circ.$

Andrew Hayes Staff - 4 years ago

My solution folds all pieces upward from the original plane, some $180^\circ$ some $90^\circ$ , and then continues folding in that direction.

Marta Reece - 4 years ago

Your solution was good to got us thinking. Here's a link to our solution: http://b3d.drjimo.net/3d-solids/9-grid-cube-problem/

Jim Olsen - 4 years ago

I thought the cube must stayed in that position. You said "this condition" and with the picture like that. You should put the notes that tell reader about that.

Beny Hakim - 4 years ago

Marta Reece
May 16, 2017

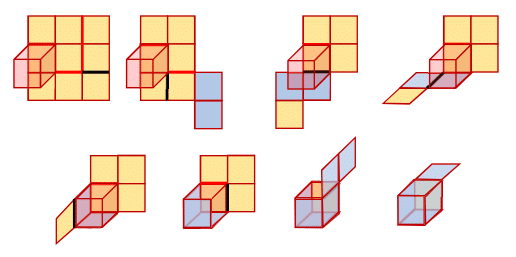
Top of the paper is shown in tan, bottom in blue. Red lines represent cuts, while black lines show the location of the next fold to be done. The cube need not be moved at all, it is certainly in contact with the middle square. It was placed differently to make the folding easier to document.

The first fold takes two squares and folds them over the top. The second takes total of four squares (now appearing as three) and folds them, also over the top. (Folding them the other way, in both cases, would work just as well.)

The bottom group of squares is folded up $90^\circ$ from the four tan ones, then the two blue squares are folded relative to each other also at $90^\circ$ to form a corner. The left tan tab is folded in $90^\circ$ .

The three squares making most of the back wall are folded to form the right wall. The top two squares are then folded down over the cube. At this point the cube is covered, but one more move can be made to make the paper into a cube.

I like this solution. I find the pictures more useful in this explanation.

Richard Desper - 4 years ago

The pictures are definitely a much better way to explain the solution visually. Well done.

Donnie Adams - 4 years ago

Actually, Marta and Donnie (above) are THE SAME solution. Outstanding! Now I've been given insight into wrapping packages (gift, shipping)

Stephen Garramone - 4 years ago

John Stegall
May 14, 2017

Move the cube to the edge of the paper

Moderator note:

Moving the cube is not prohibited; however, as pointed out in the comments, this answer does not work because the base is left uncovered.

Inadequate description of rules. Misleading

Jeff Hultman - 4 years ago

Could you explain what you are misled by? Moving the cube is allowed.

Jason Dyer Staff - 4 years ago

In my case I was not counting with the possibility of moving the cube, maybe it was my fault. Thanks

Guillermo Callaghan - 4 years ago

poor question - inadequate rules

David Fleming - 4 years ago

Since you are not allowed to separate the pieces there is no way to get four squares in a row which would somewhere have to take place in order to cover the bottom, back, top, and front.

Lowell Beal - 4 years ago

Agree. There needs to be four squares in a row.

Bernie Cass - 4 years ago

Check out @Donnie Adams solution. It can be done!

Andrew Hayes Staff - 4 years ago

Does this solution mean moving the cube off that paper? This still leaves the base uncovered.

Tom Anlezark - 4 years ago

4 squares in a row are not required (to côver the cube)

Jim Olsen - 4 years ago

I'm guessing (like Tom Anlezark has guessed in the comment below) you are leaving the base unwrapped; the problem states "the entire cube" which refers to every part, including the base.

Jason Dyer Staff - 4 years ago

"Move the cube to the edge of the paper"...and what?

Richard Desper - 4 years ago

I see. I was under the impression you weren't allowed to move the cube in this problem.

Deva Craig - 4 years ago

Moving the cube is allowed. Moving the cube without cutting will not solve the problem.

Jason Dyer Staff - 4 years ago

As you can see from the solution I posted, moving the cube is not needed. That makes sense, given the fact that the cube is surrounded by so many squares, one of them being the central one.

Marta Reece - 4 years ago

A horribly written question! No where does it suggest that moving the paper or the cube is allowed. By adding the two additional conditions, it further implies that moving the cube is NOT one of the conditions.

Daniel Kantor - 4 years ago

The actual correct solutions (the two above this one) work with or without moving the cube.

Jason Dyer Staff - 4 years ago

I believe that the question was ambiguously worded. Yes, moving the cube was not prohibited - and I thought of doing it, but the first sentence "We have a 1x1x1 orange cube on a piece of 3x3 blue paper. " certainly implied that the starting point had to be as shown in the picture. Poor wording takes the fun out of the puzzle.

Christopher Hoeber - 4 years ago

However, the solution does not require the cube to be moved.

Marta Reece - 4 years ago

Derek Foster
May 15, 2017

Agree with John Steghall. Visuallise it. Used to wrapping Xmas gifts on 'justenough' paper sheets.

You have nine square units of paper and only need six units to cover the cube. The issue is what cuts are allowed.

Richard Desper - 4 years ago

Kunal Kundwani
May 14, 2017

Keep the cube with just one vertex touching the paper

Number the squares first row left to right 1 2 3. 2nd row 4, 5, 6. 3rd row 7,8,9. Move cube onto square 1. Cut to separate 2,3 from 5,6. Cut off 8,9. fold 2, 3 underneath so 2 doubles up and 3 cover left face. Fold 4, 7 so 7 covers top. Fold 5, 6 around to cover remaining two faces. Done

John Savage - 4 years ago

Donald Zacherl
May 21, 2017

Hints for an elegant solution: 1. Start by unfolding cube, not by folding paper. 2. Use symmetry. 3. There are 6 cubic faces and 9 paper squares, so as many as 4 paper squares will be in at least one superposition on cubic face. 4. Remember that paper folds both ways.

Matt Roberts
May 18, 2017

This is why I call it a Qu-bit of measuring?

Can you explain what's a Qu-bit of measuring?

Christopher Boo - 4 years ago

Bob Liddington
May 18, 2017

No cutting required!

Rotate cube by 45°
Grab 4 corners of paper and bring to top of cube.

Since the length of the diagonal is 3 x root 2 = 4.24 and the there are only 4 units of (rotated) cube to cover there is plenty of overlap.

Not exactly elegant, but effective.

Whoops! "Can only be ...folded along the grid". Too bad

Wrap the cube

8 solutions

Moderator note:

Moderator note:

0 pending reports