Wrecked angles

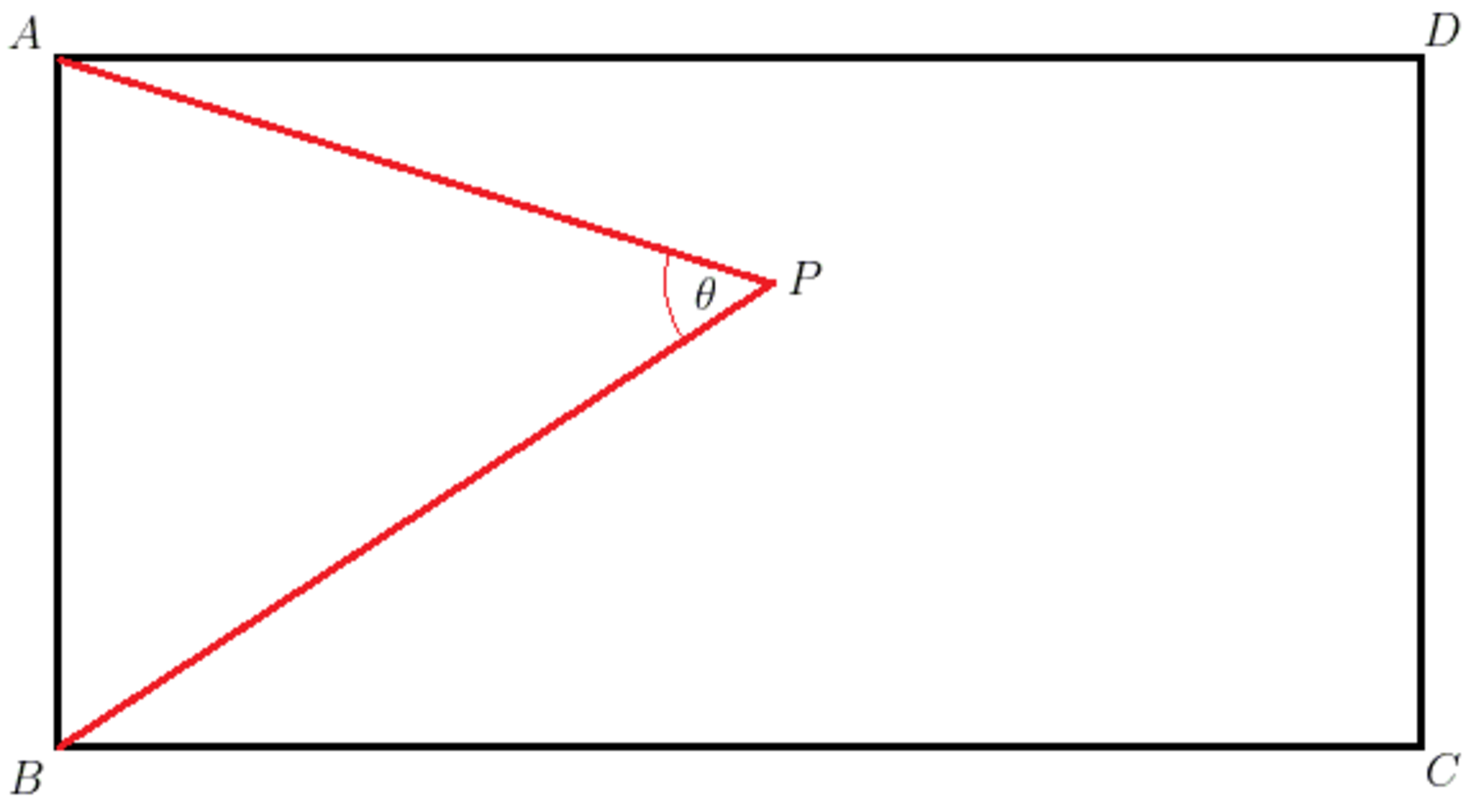
Let's look at the general problem, where $AB=1$ and $BC=b$ (only the ratio of the sides matters). If we take the point $B$ as an origin, with $x$ -axis along $BC$ , and let $P$ have coordinates $(x,y)$ , then we find $\theta=\tan^{-1}\frac{y}{x}+\tan^{-1}\frac{1-y}{x}$

To find the expected value of $\theta$ , we need to evaluate $E(\theta)=\frac{1}{b} \int_0^b \int_0^1 \tan^{-1}\frac{y}{x}+\tan^{-1}\frac{1-y}{x} dy \; dx$

This is unpleasant, but not impossible; after a bit of wrangling, we find $E(\theta)=2 \cot^{-1} b + b \log b + \frac{b^2-1}{2b} \log(b^2+1)$

For the particular case $b=1+\sqrt2$ , we have $2 \cot^{-1} b=\frac{\pi}{4}$ . Also, $b$ satisfies $b^2-1=2b$ . Finally, using the identity $\sinh^{-1} z = \log \left(z+\sqrt{1+z^2}\right)$ gives $\log b=\sinh^{-1} 1$ . Putting all this together, $E(\theta)=\frac{\pi}{4}-\frac{3\log 2}{2} + \sqrt{2} \sinh^{-1} 1$

or $a=4,b=3,c=2,d=1$ , so that $a+b+c+d=\boxed{10}$ .