The Conical X-Factor

Geometry Level 3

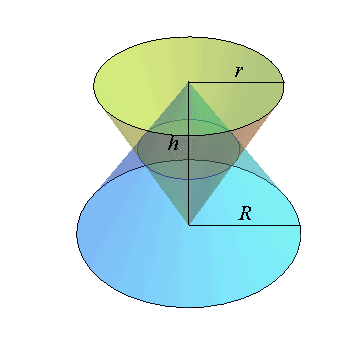
Two right circular cones each share the same altitude and a height of h h . One cone has a base of radius R R and the other cone is inverted and has a base of radius r r as shown in the figure below.

The volume of the region common to both cones can be calculated by the formula:

V = π R 2 r 2 h X ( R + r ) 2 V =\frac {\pi R^2 r^2 h}{ X ( R + r )^2}

Find X X .


The answer is 3.

W Rose by W Rose , 63, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Tom Engelsman
Nov 17, 2016

6 Helpful 0 Interesting 0 Brilliant 0 Confused
Dan Ley
Dec 29, 2016

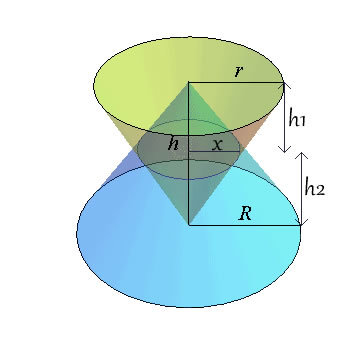
By ratios, x r = h 2 h \frac{x}{r}=\frac{h_2}{h} and similarly x R = h 1 h \frac{x}{R}=\frac{h_1}{h}

⟹ x h R + x h r = h 1 + h 2 = h \implies \frac{xh}{R}+\frac{xh}{r}=h_1+h_2=h

Dividing by h h and cross-multiplying gives x = R r R + r x=\frac{Rr}{R+r}

The area of intersection is 1 3 π x 2 h 1 + 1 3 π x 2 h 2 = 1 3 π x 2 ( h 1 + h 2 ) = 1 3 π x 2 h \frac{1}{3}\pi x^2h_1 + \frac{1}{3}\pi x^2h_2= \frac{1}{3}\pi x^2(h_1+h_2)=\frac{1}{3}\pi x^2h

If we substitute in x 2 x^2 we get 1 3 π h R 2 r 2 ( R + r ) 2 = π R 2 r 2 h 3 ( R + r ) 2 ⟹ X = 3 \frac{1}{3}\pi h\frac{R^2r^2}{(R+r)^2}=\frac{\pi R^2r^2h}{3(R+r)^2} \implies X=3

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...