$x$ and $y$ are the friendly enemies

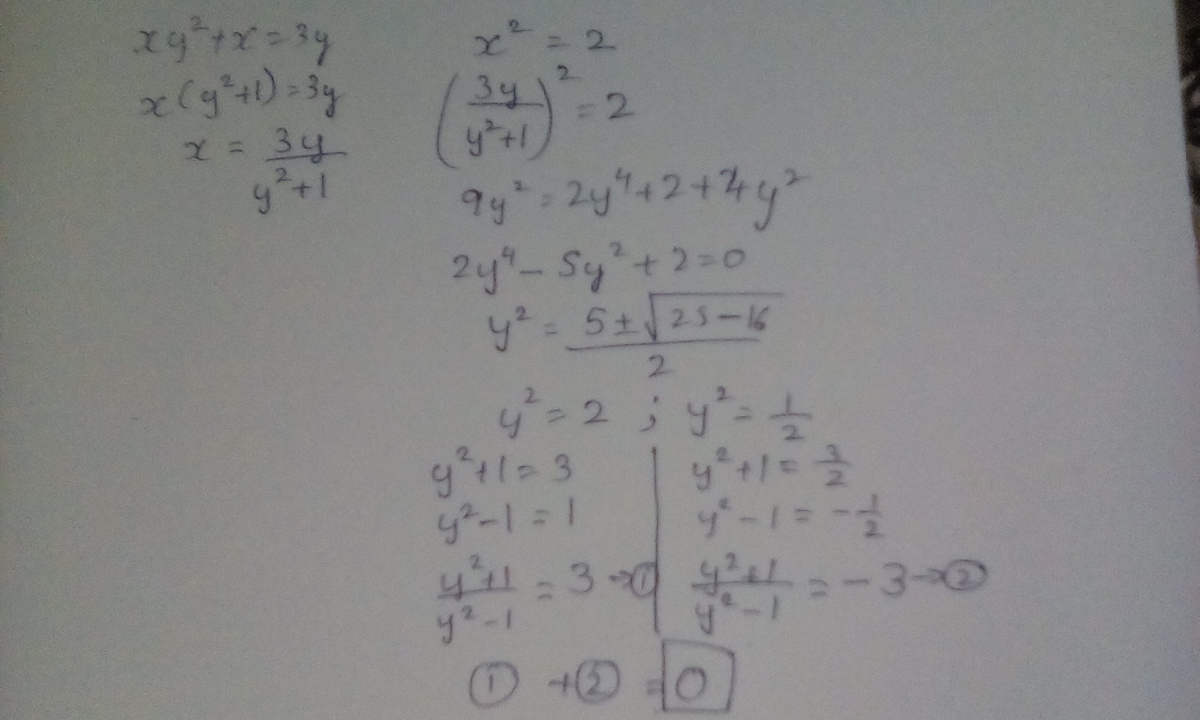
Given $xy^2+x=3y$

$\implies$ $xy+\dfrac{x}{y}=3$ $\rightarrow$ $(i)$ (dividing throughout by $y$ since $y\neq0$ )

Also $xy(\frac{x}{y})=2$ $\rightarrow$ $(ii)$

Now, $xy$ and $\frac{x}{y}$ are the roots of a quadratic equation whose sum and product of roots are known which are given above as the $2$ equations.

Let the QE be in some variable $p$

Therefore, the QE is $p^2-3p+2=0$

$\implies$ $(p-1)(p-2)=0$

Now the roots are $1$ and $2$ .

Here, $2$ cases are possible.

---

$\rightarrow$ $\text{case(i)}$

$xy=1$ and $\dfrac{x}{y}=2$

$\dfrac{xy}{\frac{x}{y}}=\dfrac{1}{2}$

$y^2=\dfrac{1}{2}$

Applying Componendo-Dividendo and simplifying, we get

$\dfrac{y^2+1}{y^2-1}=\boxed{-3}$

---

$\rightarrow$ $\text{case(ii)}$

$xy=2$ and $\dfrac{x}{y}=1$

$\dfrac{xy}{\frac{x}{y}}=\dfrac{2}{1}$

$y^2=\dfrac{2}{1}$

Applying Componendo-Dividendo and simplifying, we get

$\dfrac{y^2+1}{y^2-1}=\boxed{3}$

---

Hence the sum of all possible values is $-3+3=\boxed{0}$